Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Aritmética de Ponto Flutuante

Ver Todos os Exercícios

Teoria

Fala aí, beleza?! Vamos falar sobre a linguagem que os computadores usam?! Um computador ou calculadora representa um número real no sistema denominado aritmética de ponto flutuante! Os números binários são representados seguindo um padrão seguido por praticamente todos os computadores:

Uma representação binária em 32   b i t s (precisão simples) é usada para números reais, onde temos 1 bit para o sinal, 8 para a característica e 23 para a mantissa (parte fracionária do número). Nesse caso, o expoente varia entre - 126 até 127 .

Em geral, um número normalizado em 32 bits é da forma:

- 1 s 2 c - 127 1 + f

Onde s será o sinal, c a característica e f a mantissa.

Se estivermos trabalhando com 64 bits o 127 é substituído por 1023. Beleza?!

Obs.: Alguns valores especiais são:

z e r o → s = 0   o u   1 ; e x p = 0 ; f = 0

+ ∞ → s = 0 ; e x p = 111 … 111 ; f = 0

- ∞ → s = 1 ; e x p = 111 … 111 ; f = 0

N a N   n o t   a   n u m b e r → s = 0   o u   1 ; e x p = 111 … 111 ; f ≠ 0

Quando temos o expoente igual a 0 e um valor diferente de 0 na mantissa é uma indicação de número não normalizado. Nesse caso consideramos a mantissa entre 0 e 1 ao invés de entre 1 e 2 e usamos o expoente mínimo. Na aritmética de ponto flutuante ficamos com essa carinha aqui, onde:

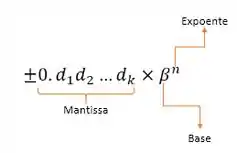
Os d i ' s são os dígitos da parte fracionária:

1 ≤ d 1 ≤ β - 1

0 ≤ d i ≤ β - 1   ,   i ∈ 2 , k

β é a base (em geral 2, 10 ou 16);

k é o número de dígitos na mantissa;

n é o expoente no intervalo 1 , u

Show de bolas?!

Desse modo, uma máquina que use aritmética de ponto flutuante pode ser caracterizada por 4 números:

F β , k , e m i n , e m a x

Vamos ver um exemplo de como isso funciona?

Considere, por exemplo, uma máquina que opera no sistema:

β = 10 ; k = 5 ; n ∈ - 5,5 ,

Ou seja, F 10,5 , - 5,5 . Os números são representados neste sistema da seguinte forma:

± 0 . d 1 d 2 d 3 d 4 d 5 × 10 n ; 1 ≤ d 1 ≤ 9 ;   0 ≤ d i ≤ 9   ,   i ∈ 2,5

O menor número, em valor absoluto, representado por essa máquina seria:

0.10000 × 10 - 5 = 10 - 6

Enquanto o maior número seria:

0.99999 × 10 5 = 99999

Show de bola?!

Como vimos, em nenhuma máquina é possível representarmos todos os números reais devido ao limite físico. Sendo assim apenas um conjunto deles pode ser representado completamente. Por essa razão, a representação de alguns números será realizada por meio de truncamento ou arredondamento.

Por exemplo, o número π é representado na sua forma decimal normalizada da seguinte forma:

π = 0.314159265 … × 10 1

Se fôssemos representa-lo na máquina acima usando truncamento teríamos:

0.31415 × 10 1

Enquanto usando arredondamento teríamos:

0.31416 × 10 1

Isso porque o sexto dígito da representação normalizada de π é um 9 ≥ 5 , logo ao arredondarmos somamos uma unidade na quinta casa decimal. Beleza?!

Nesse caso temos que π está entre o mínimo e máximo que essa máquina pode representar, mas possui muitas casas decimais, então acabamos com uma aproximação.

Também pode acontecer de termos um número menor que o mínimo da máquina, como por exemplo:

0.97976 × 10 - 7

Ele não pode ser representado pois o expoente n é menor que - 5 . Nessas situações a máquina acusa a ocorrência de underflow. Analogamente podemos ter um número de valor absoluto maior do que a máquina consegue representar:

0.60963 × 10 8

Nesse caso a máquina acusa a ocorrência de overflow. Beleza, vamos praticar um pouco isso aí que vimos antes de passar adiante!

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Considere um computador de 16   b i t s com expoente máximo e = 31 e a representação em aritmética flutuante na base 2 .

a Determine o menor número positivo normalizado e não normalizado representável nesta máquina, na base 10 .

b Determine o maior número positivo representável nesta máquina, na base 10 .

Passo 1

Antes de qualquer coisa temos que descobrir quantos b i t s essa máquina reserva para cada coisa. Temos 1 b i t pro sinal. Para que o expoente máximo seja 31 , usando nossa relação:

31 = 2 n . e . - 1 - 1

log 2 ⁡ 32 = n . e . - 1

5 = n . e . - 1

n . e . = 6

Logo, temos 6 b i t s   para o expoente.

Ficamos então com:

16 - 6 - 1 = 9

Logo, 9   b i t s para a mantissa.

Passo 2

a O menor número normalizado representável seria:

0   000001   000000000

Equivalente em decimal a:

- 1 0 ∙ 2 - 30 ∙ 1 ≈ 9.313226 × 10 - 10

Já o menor número não normalizado seria:

0   000000   000000001

Equivalente a:

- 1 0 ∙ 2 - 30 ∙ 0.001953125 = 1.818989 × 10 - 12

Passo 3

b O maior número positivo representável é:

0   111110   111111111

O que equivale a:

- 1 0 ∙ 2 31 ∙ 1 . 998046875 = 4.290772992 × 10 9

Resposta

a Menor número positivo normalizado: 9.313226 × 10 - 10

Menor número positivo não normalizado: 1.818989 × 10 - 12

b Maior número positivo: 4.290772992 × 10 9

Exercício Resolvido #2

Lista 1 – Professora Luziane – UFRJ – Questão 1 e 2 Adaptadas

Expresse os números a seguir usando representação em ponto flutuante normalizada na base indicada:

a 5.987 10

b 630 10

c 0.000000512 10

d 1111 2

e 10.11 2

f 0.0001000 2

Em seguida, refaça o exercício usando apenas 2 dígitos na mantissa e arredondamento.

Passo 1

a 5.987 10 = 0.5987 × 10 1

b 630 10 = 0.63 × 10 3

c   0.000000512 10 = 0.512 × 10 - 6

d 1111 2 = 0.1111 × 2 4

e 10.11 2 = 0.1011 × 2 2

f   0.0001000 2 = 0.1 × 2 - 3

Passo 2

Refazendo com 2 dígitos na mantissa e arredondamento.

a 5.987 10 = 0.60 × 10 1

b 630 10 = 0.63 × 10 3

c   0.000000512 10 = 0.51 × 10 - 6

d 1111 2 = 0.1 1 × 2 4

e 10.11 2 = 0.1 0 × 2 2

f   0.0001000 2 = 0.10 × 2 - 3

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Lista 1 – Professora Angela – UFRJ – Questão 4 Adaptada

Seja um computador binário cuja palavra tem 3 dígitos para a mantissa, característica variando de m = - 2 a M = 2 e que trabalha com truncamento.

a Calcule o menor número negativo nele representável.

b Calcule o maior número positivo nele representável.

c O número 11 8 está entre os números calculados em a e b ?

Passo 1

O menor número negativo é simplesmente o maior número positivo com o b i t de sinal trocado né haha. Então podemos responder a a e a b de uma vez! Como o maior expoente é 2 , o maior número positivo em binário seria:

0.111 × 2 2 = 11.1

O menor número negativo seria em binário:

- 0.111 × 2 2 = - 11.1

Passo 2

Agora ele quer saber se 11 8 = 1.375 está entre os valores que achamos. Como não podemos comparar um número no sistema decimal com um no binário, vamos converter 1.375 para binário:

1 10 = 1 2

0.375 × 2 = 0.75 → D í g i t o   0

0.75 × 2 = 1.5 → D í g i t o   1

0.5 × 2 = 1 → D í g i t o   1

0.375 10 = 0.011 2

Logo,

1.375 10 = 1.011 2

Ou seja, ele está entre os valores encontrados nas letras a e b .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

Lista 1 – Professor Raymundo – UFRJ – Questão 10a

Seja um computador binário, cujo sistema de ponto flutuante tenha 1   b i t para o sinal do número, 5   b i t s para o expoente e 6   b i t s para a mantissa num total de 12   b i t s . Qual o menor número positivo e o maior número positivo nele representável.

Passo 1

Como temos 5   b i t s para o expoente, o expoente máximo é dado por:

e m a x = 2 5 - 1 - 1 = 2 4 - 1 = 15

Portanto, o expoente mínimo será - 14 .

Também podemos pensar que a máquina vai do expoente 00001 até o 11110 , ou seja, do 1 ao 30 . Como queremos representar os números negativos também, subtraímos 15 , de modo que os expoentes agora variam de - 14 até 15 .

Passo 2

Para obter o maior número, devemos ter o maior expoente e a maior mantissa.

- O maior expoente: 15

- A maior mantissa: f= 0. (111111)

Colocando a mantissa na base decimal:

0.111111 2 = 2 - 1 + 2 - 2 + 2 - 3 + 2 - 4 + 2 - 5 + 2 - 6 = 2 0 - 2 - 6

O valor máximo é dado por:

2 15   ∙   1 + 2 0 - 2 - 6

Sendo assim, o valor máximo que ela pode representar é:

2 15 ∙ 2 - 2 - 6 = 65024

Passo 3

O valor mínimo normalizado é dado por:

- O menor expoente: -14

- A menor mantissa: f= . (000000)

Observação: Só podemos ter essa mantissa toda 0 porque o valor normalizado já conta com um dígito 1 antes da vírgula.

Assim, o valor mínimo normalizado será:

2 - 14   ∙   1 + 0 = 2 - 14 = 6.103515625   x   10 - 5

Passo 4

O valor mínimo não normalizado é bem parecido, mas tem a seguinte diferença: não tem aquele 1 antes da vírgula. Então, para obter o valor mínimo, devemos considerar 0 antes da vírgula e o máximo de 0s possíveis na mantissa, colocando 1 apenas no dígito de menor valor. Assim:

- A menor mantissa: f= 0. (000001)

Passando a mantissa para a base decimal:

2 - 6

Assim, o menor valor não normalizado é dado por:

2 - 14   ∙   2 - 6 = 2 - 20 = 9.53674316   x   10 - 7

Resposta

Maior número positivo: 65024

Menor número positivo normalizado: 6.103515625 × 10 - 5

Menor número positivo não normalizado: 9.5367431640625 × 10 - 7

Exercício Resolvido #5

Lista 1 – Professora Luziane – UFRJ – Questão 3

Suponha que estejamos usando uma máquina que funciona em base 2 e possui uma representação em 10   b i t s , sendo 1 para o sinal da mantissa, 3 para o expoente e 6 para a mantissa. A partir de que valor a máquina irá exibir na resposta o v e r f l o w ? E u n d e r f l o w ?

Passo 1

Para descobrirmos que números causam o v e r f l o w e u n d e r f l o w na máquina precisamos saber o número máximo que ela consegue representar, assim como o número mínimo.

Como temos 3   b i t s para o expoente, o expoente máximo é dado por:

e m a x = β n - s - 1 = 2 3 - 1 - 1 = 2 2 - 1 = 3

Onde   β é a base, n   é a quantidade de bits para o expoente e s é a quantidade de bits para o sinal da mantissa.

Também podemos pensar que a máquina vai do expoente 001 até o 110 , ou seja, do 1 ao 6 . Como queremos representar os números negativos também, podemos subtrair 3 para encontrar o expoente mínimo.

Então, o expoente mínimo será - 2 , de modo que os expoentes agora variam de - 2 até 3 .

Passo 2

Sendo assim, o valor máximo que ela pode representar é:

2 3 ∙ 2 - 2 - 6 = 15.875

Qualquer valor maior que esse causará o v e r f l o w .

Já o valor mínimo será:

2 - 2 ∙ 1 = 0.25

Qualquer valor menor que esse em módulo causará u n d e r f l o w .

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #6

Adaptado da lista “Cálculo Numérico (ST462B/ST468B) Lista de exercícios 1 - Representação numérica e Erros” da Unicamp

Considere uma máquina cujo sistema de representação de número é definido por: 𝛽 = 10, 𝑘 = 4,𝑒 ∈ [−5,5]. Pede-se:

(a) Qual o menor e o maior número em módulo representados nesta máquina?

(b) Como será representado o número 73,758 nesta máquina, se for usado o arredondamento? E se for usado o truncamento?

Passo 1

(a) Qual o menor e o maior número em módulo representados nesta máquina?

Opaa, chega mais ! Vamos começar com esse exercício que parece moleza mas é cheio de detalhes. Tem um palpite de como se começa??

Veja bem, que informações o exercício nos dá? O problema nos fornece a base, o número máximo de algarismos que vamos colocar na mantissa e os valores mínimos e máximos de expoente (no intervalo de -5 até 5).

Então, vamos relembrar aquela estrutura que pode ser montada só com as informações que nós temos:

Sabendo que: 1 ≤ d 1 ≤ β - 1

Nós conhecemos o valor de β = 10

Então, considerando a inequação acima podemos determinar o primeiro valor de d 1

Que pode deve estar entre 1 e 9.

1 ≤ d 1 ≤ 9

Fácil né? Então significa que podemos variar o nosso valor de (0,1....   d k ) até (0,9...   d k ).

O exercício fornece que k= 4, então nossos valores de d serão: d 1 , d 2 ,   d 3   e   d 4 .

Para montar a estrutura do menor valor que a máquina pode registrar, devemos considerar que o primeiro dígito d 1 ≠ 0 (qualquer zero a esquerda acaba sendo reconsiderado e reorganizado e vai parar laaaaaaaaaaaá no expoente) , e como determinamos ali em cima ele deve estar entre 1 e 9.

Como o menor valor entre 1 e 9, é o próprio 1 nosso d 1 = 1 assumirá essa forma.

Beleza, o β = 10 e n= [-5,5].

A escolha do menor expoente é bem intuitiva né, qual é o menor valor -5 ou 5?

O menor valor é -5, heheheh

Agora é só montar aquela estrutura show de bola:

Lembra, nós temo as base, expoentes e d 1 . Mano, agora é só completar!!

O menor número, em valor absoluto, representado por essa máquina seria:

0.1000 × 10 - 5 = 10 - 6

Enquanto o maior número seria:

0.9999 × 10 5 = 99990

Moleza né???

Vamos para o próximo passo!

Passo 2

(b) Como será representado o número 73,758 nesta máquina, se for usado o arredondamento? E se for usado o truncamento?

Ao organizarmos o número 73,758 no formato da aritmética de ponto flutuante, fica mais ou menos assim:

0.73758 × 10 2

Mas, nós temos que deixar com a quantidade correta de números dentro da mantissa que foi sugerida pelo exercício de k= 4.

Vamo simbora!

Só dando uma relembrada como eu faço o arredontamento?

O arredondamento com k dígitos é dado por:

Se d k + 1 ≥ 5 arredondamos para cima.

Se d k + 1 < 5 arredondamos pra baixo!

Legal, foca nesse número 0.73758 , a certeza que temos está em 0,737X , com 3 algarismos significativos e o último duvidoso!

E agora observe bem: 0.737 58 o próximo algarismo em d k + 1 ≥ 5 e então arredondamos para CIMA!

Então, com a técnica de arredondamento fica assim:

0.7376 × 10 2

No truncamento fica como?

No truncamento nós terminamos em d k =   d 4

Observe que temos:

0.73758 × 10 2

Ao para em d 4 para fazer o truncamento, fica assim:

0.7375 × 10 2

Resposta

  1. Mínimo: 0.1000 × 10 - 5 = 10 - 6

    2. Máximo: 0.9999 × 10 5 = 99990

  2. Arredondamento : 0.7376 × 10 2

Truncamento : 0.7375 × 10 2

Exercício Resolvido #7

Lista 1 – Professor Daniel – UFRJ – Questão 3

Considere uma máquina com sistema de representação de números definido por: base 10 , 5 dígitos na mantissa e expoente no intervalo - 6 ; 6 . Como será representado o número 1892477 nesta máquina se for usado o arredondamento. E se for usado o truncamento?

Passo 1

Nosso instinto já manda a gente fazer o que? Passar pra binário né? Mas presta atenção no que o enunciado fala!! Ele diz que a máquina funciona na base 10 ! Então não tem que passar nada pra nada haha. É só passar pra notação normalizada de ponto flutuante:

1892477 = 0.1892477 × 10 7

Usando o truncamento temos:

0.18924 × 10 7

E usando o arredondamento:

0.18925 × 10 7

Repare que, como temos um expoente maior que o expoente máximo da máquina, ela acusaria overflow!

Resposta

Truncamento: 0.18924 × 10 7

Arredondamento: 0.18925 × 10 7

A máquina acusaria overflow.

Exercício Resolvido #8

Lista 1 – Professor Raymundo – UFRJ – Questões 3 até 7

Um computador armazena números reais utilizando 1   b i t para o sinal do número, 7   b i t s para o expoente e 8   b i t s para a mantissa. Admitindo que haja arredondamento, como ficariam armazenados os seguintes números decimais?

a 265

b 12.5

c - 445.25

d - 0.1

e - 12.8

f 2500.05

Em seguida, responda:

i Qual o valor verdadeiramente representado em cada caso acima?

i i Qual o maior e o menor número positivo nele representável?

i i i Qual o menor número maior que 100 nele representável?

i v Qual o maior número menor que 20 nele representável?

Passo 1

Os 7   b i t s do expoente variarão de 0000001 até 1111110 , isto é, de 1 até 126 . Como precisamos representar expoentes negativos, subtraímos 63 disso de modo que o expoente agora varie de - 62 até 63 .

a 265

Passando o número para binário.

265 2 = 132   e   r e s t o   1

132 2 = 66   e   r e s t o   0

66 2 = 33   e   r e s t o   0

33 2 = 16   e   r e s t o   1

16 2 = 8   e   r e s t o   0

8 2 = 4   e   r e s t o   0

4 2 = 2   e   r e s t o   0

2 2 = 1   e   r e s t o   0

1 2 = 0   e   r e s t o   1

265 10 = 100001001 2

Então, 265 10 = 100001001 2 = 1 . 00001001 × 2 8 . Repare que esse 1 na frente do binário é aquele 1 que sempre somamos e está implícito. Na hora de passar ele para a representação passamos só o que ficou depois da vírgula. Além disso, como temos 8   b i t s mantissa e 8 casas decimais, não precisaremos cortar nenhuma.

Quanto ao expoente 8 , precisamos somar aqueles 63 que calculamos para obtermos o expoente certo.

8 + 63 = 71 = 64 + 4 + 2 + 1 = 2 6 + 2 2 + 2 1 + 2 0

A representação no sistema será:

0   1000111   00001001

Passo 2

b 12.5

Passando o número para binário. Primeiro a parte inteira:

12 2 = 6   e   r e s t o   0

6 2 = 3   e   r e s t o   0

3 2 = 1   e   r e s t o   1

1 2 = 0   e   r e s t o   1

12 10 = 1100 2

Agora a parte fracionária:

0.5 × 2 = 1 → D í g i t o   1

Então, 12.5 10 = 1100.1 2 = 1 . 1001 × 2 3 . Temos 8   b i t s mantissa e 4 casas decimais, então não precisaremos cortar nenhuma.

Consertando o expoente:

3 + 63 = 66 = 64 + 2 = 2 6 + 2 1

A representação no sistema será:

0   1000010   10010000

Passo 3

c - 445.25