Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 5.Exercícios - Ex. 13

13. Sendo p n x = ∑ k = 0 n L k x f ( x k ) o polinômio que interpola f ( x ) em x 0 , x 1 , … . , x n na forma de Lagrange mostre que...

∑ k = 0 n L k ( x ) = 1 ,   ∀ x

(Sugestão: Interpole a função f x = 1 .)

Passo 1

E ai meu bom!

Veja só! Segundo esse esquema que propõe o enunciado, teríamos mais ou menos o exposto na seguinte tabela...

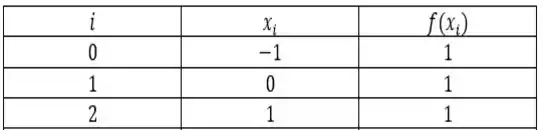
Ou seja, para todo x , a função f ( x i ) vai ser igual a 1 .

O que a gente tem aí, são 2 nós de interpolação! Por isso, vamos pegar um polinômio de seundo grau, dado por...

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2

Passo 2

Agora, vamos calcular os termos L 0 , L 1 , L 2 e L 3 ...

Quem manda no L 0 é o grau 0 , então o x 0 fica no quociente e manda sempre subtrair os outros termos! Fica assim...

L 0 = ( x - x 1 ) ( x - x 2 ) ( x 0 - x 1 ) ( x 0 - x 2 )

L 0 = ( x ) ( x - 1 ) ( - 1 ) ( - 2 ) = x 2 - x 2

O L 1 por sua vez fica assim...

L 1 = ( x - x 0 ) ( x - x 2 ) ( x 1 - x 0 ) ( x 1 - x 2 )

L 1 = ( x + 1 ) ( x - 1 ) ( 1 ) ( - 1 ) = - x 2 + 1

Já O L 2 :

L 1 = ( x - x 0 ) ( x - x 1 ) ( x 2 - x 0 ) ( x 2 - x 1 )

L 1 = x + 1 x 2 = x 2 + x 2

Passo 3

Agora, juntamos tudo no polinômio...

p 2 x = y 0 L 0 + y 1 L 1 + y 2 L 2

p 2 x = 1 ⋅ x 2 - x 2 + 1 ⋅ x 2 - 1 + 1 ⋅ x 2 + x 2

p 2 x = x 2 - x 2 + - x 2 + 1 + x 2 + x 2

p 2 x = 1

Ou seja! No final das contas, o polinômio interpolador sempre vai dar 1 , conforme o que propõe o enunciado! Isso independe do grau do polinômio e do tanto de pontos que a gente pega!

Resposta

∑ k = 0 n L k ( x ) = 1 ,   ∀ x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja a tabela: Usando um polinômio interpolador de grau 2, trabalhe de dois modos diferentes para obter o valor estimado de x para o qual f(x) = 0.23. Dê uma estimativa do erro cometido em cada caso,
Construir os polinômios de interpolação, na forma de Lagrange, para a função y = sin ⁡ π x , escolhendo os pontos: x 0 = 0;x 1 = 1 6;x 2 = 1 2.
Sabendo-se que e = 2 , 72 ,e = 1 , 65 e que a equação x-e - x =0 tem uma raiz em [ 0 ,1 ] , determinar o valor dessa raiz, usando a Fórmula de Lagrange sobre 3 pontos.
Calcular e 3 , 1 usando a Fórmula de Lagrange sobre 3 pontos e a tabela:Observe que como queremos e 3,1 usando 3 pontos, devemos escolher 3 pontos consecutivos na vizinhança de 3 , 1 . Assim temos dua