Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 5.Exercícios - Ex. 10

Seja a tabela:

Usando um polinômio interpolador de grau 2, trabalhe de dois modos diferentes para obter o valor estimado de x para o qual f(x) = 0.23. Dê uma estimativa do erro cometido em cada caso, se possível

Passo 1

Então, os dois modos que vamos resolver essa questão são o seguinte. Primeiro, vamos encontrar uma função de interpolação para f ( x ) e igualar a 0.23.

O segundo modo é meio não usual e normalmente não passaria pela cabeça da gente. Por que não interpolarmos x   como função de y ao invés de y como função de x? Nesse caso, bastaria substituirmos 0.23 na nossa função de interpolação!

Passo 2

Vamos começar pelo primeiro modo! Como queremos um polinômio interpolador de grau 2 precisamos de três pontos. Vamos usar esses aqui:

x 0 = 0.25

x 1 = 0.30

x 2 = 0.35

Temos então que:

p 2 ( x ) = y 0 L 0 + y 1 L 1 + y 2 L 2

onde:

y 0 = f ( x 0 ) = 0.19

y 1 = f ( x 1 ) = 0.22

y 2 = f ( x 2 ) = 0.25

L 0 = ( x - x 1 ) ( x - x 2 ) ( x 0 - x 1 ) ( x 0 - x 2 ) = 200 x 2 - 130 x + 21

L 1 = ( x - x 0 ) ( x - x 2 ) ( x 1 - x 0 ) ( x 1 - x 2 ) = - 400 x 2 + 240 x - 35

L 2 = ( x - x 0 ) ( x - x 1 ) ( x 2 - x 0 ) ( x 2 - x 1 ) = 200 x 2 - 110 x + 15

Logo,

p 2 ( x ) = 15 x + 1 25

Repare que aqui os x 2 se cancelaram! Por isso que ela não está do segundo grau. O próximo passo é igualarmos ela a 0.23 para acharmos o x :

15 x + 1 25 = 0.23

15 x + 1 = 5.75

x = 0.31667

Passo 3

Agora vamos reescrever essa tabela com x sendo função de y:

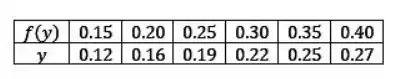
Agora vamos encontrar a função de interpolação de f(y):

y 0 = 0.19

y 1 = 0.22

y 2 = 0.25

Temos então que:

p 2 ( y ) = x 0 L 0 + x 1 L 1 + x 2 L 2 ,

onde,

x 0 = f ( y 0 ) = 0.25

x 1 = f ( y 1 ) = 0.30

x 2 = f ( y 2 ) = 0.35

L 0 = ( y - y 1 ) ( y - y 2 ) ( y 0 - y 1 ) ( y 0 - y 2 ) = 555.556 y 2 - 261.111 y + 30.5556

L 1 = ( y - y 0 ) ( y - y 2 ) ( y 1 - y 0 ) ( y 1 - y 2 ) = - 1111.11 y 2 + 488.889 y - 52.7778

L 2 = ( y - y 0 ) ( y - y 1 ) ( y 2 - y 0 ) ( y 2 - y 1 ) = 555.556 y 2 - 227.778 y + 23.2222

Logo,

p 2 ( y ) = 5 y - 0.2 3

Novamente os x 2 se cancelaram! E agora temos uma função de y! Então podemos

substituir direto o 0.23 e achar o x :

x = 0.31667

Resposta

x = 0.31667

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

13. Sendo p n x = ∑ k = 0 n L k x f ( x k ) o polinômio que interpola f ( x ) em x 0 , x 1 , … . , x n na forma de Lagrange mostre que... ∑ k = 0 n L k ( x ) = 1 ,∀ x (Sugestão: Interpole a função f x
Construir os polinômios de interpolação, na forma de Lagrange, para a função y = sin ⁡ π x , escolhendo os pontos: x 0 = 0;x 1 = 1 6;x 2 = 1 2.
A integral elíptica completa é definida por: K k = ∫ 0 π 2 d x 1 - k 2 sin 2 ⁡ x 1 2 Por uma tabela de valores dessa integral encontramos:K 1 =1.5708 ;K 2 = 1.5719 ;K 3 = 1.5739 Determinar K ( 2.5 ) ,
Dar uma outra prova de unicidade do polinômio de interpolação P n ( f ; x ) de uma função y= f ( x ) sobre o conjunto de pontos x 0 , x 1 , .. ., x n . D n ( x ) = P n ( f ; x ) - Q n ( f ; x ) .
Conhecendo-se a tabela:calcular um limitante superior para o erro de truncamento quando calculamos cos ⁡ 1,05 usando polinômio de interpolação sobre 4 pontos.