Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 6.Exercícios - Ex. 6

6. Ajuste os dados:

a) Usando a aproximação y ≈ 1 / ( a 0 + a 1 x ) . Faça o gráfico para 1 / y e verifique que essa aproximação é viável;

b) idem para y = a b x ;

c) compare os resultados (a) e (b)

Passo 1

a) E ai meu bom! Bora pra sexta questão desse capítulo 6!

Se liga só! Pra esse primeiro item, a gente tem a seguinte aproximação:

y ≈ 1 a 0 + a 1 x

Sendo assim, vamos utilizar a transformação abaixo, utilizando uma variável auxiliar z :

z = 1 y

Se z é 1 / y , então...

z = a 0 + a 1 x 1 = a 1 x + a 2

E então, temos a função linearizada através da relação 1 y ...

Passo 2

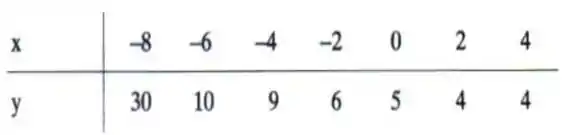
Com isso, chegamos à seguinte tabela...

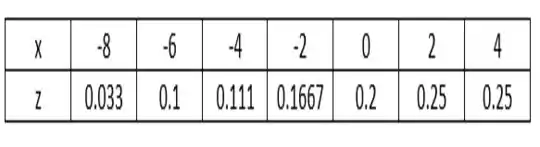
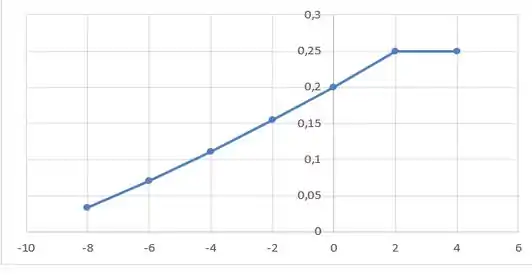
Onde plotando o gráfico, podemos ver que a melhor reta possível é dada por...

Temos então, os vetores...

h - 1 = ( 1,1 , 1,1 , 1,1 )

h - 2 = ( - 8 , - 6 , - 4 , - 2,0 , 2,4 )

f - = ( 0.033,0.1,0.111,0.1667,0.2,0.25,0.25 )

Chegando assim, à seguinte função...

y ≈ 1 0.1958 + 0.0185 x

Passo 3

b) Se a nossa função y é dada por...

y = a e x b

A nossa função de aproximação tem a forma...

ϕ x = c 1 e c 2 x

Linearizando...

z = ln ⁡ y = ln ⁡ ϕ x = ln ⁡ c 1 + ln ⁡ e c 2 x = a 1 + a 2 x

Chegamos até a seguinte tabela...

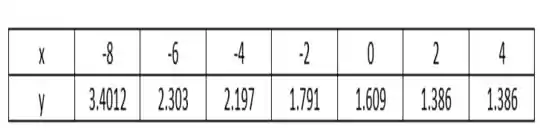
Temos então, os vetores...

h - 1 = ( 1,1 , 1,1 , 1,1 )

h - 2 = ( - 8 , - 6 , - 4 , - 2,0 , 2,4 )

f - = ( 3.4012,2.303,2.917,1.791,1.609,1.386,1.386 )

E chegamos até a seguinte função...

y ≅ 5.5199 0.8597 x

Passo 4

c) Agora vamos ver qual das duas funções garante uma melhor aproximação...

Para isso, basta plotar os pontos das duas tabelas que obtivemos em um gráfico e ver em qual situação eles estão mais perto do alinhamento...

Pois muito bem! Fazendo isso, obtemos que...

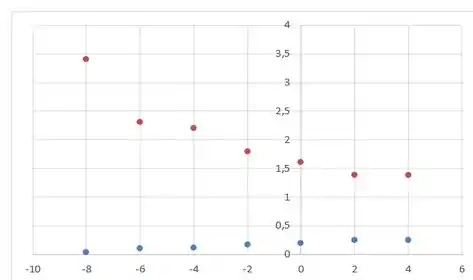
Os pontos em azul correspondem à aproximação...

y ≈ 1 a 0 + a 1 x

E os pontos em vermelho correspondem à função...

y ≅ a e x b

E como podemos ver os pontos em azul estão mais linearizados. Logo, garantem uma melhor aproximação da função.

Resposta

a)

y ≈ 1 0.1958 + 0.0185 x

b)

y ≅ 5.5199 0.8597 x

c)

A   p r i m e i r a   f u n ç ã o   g a r a n t e   u m a   m e l h o r   a p r o x i m a ç ã o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam f ( x )eg ( x ) , funções reais distintas não identicamente nulas. Suponha que, usando o método dos mínimos quadrados, aproximamos f ( x ) em [ a , b ] por: F x = a 0 f x + a 1 g ( x ) a) Quais
Considere a função dada por: a) Ajuste os pontos acima por uma função do tipo a + b x , usando o método dos mínimos quadrados.b) Qual função foi minimizada?
De uma tabela são extraídos os valores:Usando o método dos mínimos quadrados ajuste os dados acima por polinômio de grau adequado.
Achar aproximação mínimos quadrados da forma: g 1 x = a e x b e - x correspondente aos dados:
Considere a tabela:a) Pelo método dos mínimos quadrados, ajuste à tabela as funções: g 1 x = a x 2 + b x ; g 2 x = c x 2 + d b) Qual das funções fornece o melhor ajuste segundo o critério dos mínimos