Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 8.Exercícios - Ex. 20

20. Escreva a equação de 2ª ordem:

y ' ' ( x ) = 2 e 2 x - y 2 1 2 y 0 = 0 y ' 0 = 1

Como um sistema de equações de 1ª ordem e resolva-o, para x   ϵ   [ 0 ,   0.6 ] , usando h = 0.2 :

a) pelo método de Euler

b) pelo método de Euler aperfeiçoado

Passo 1

a) E aí meus caros!

Manos e Manas! Se liga só! A nossa equação é dada por...

y ' ' ( x ) = 2 e 2 x - y 2 1 2

Bom! E pra achar um sistema de equações, o que a gente precisa fazer é utilizar substituição de variáveis.

Vamos chamar y ' x   de z ( x ) . Sendo assim, ficamos com..

y ' ' x = z ' ( x )

Passo 2

E fazendo as devidas substituições na nossa EDO, de 2 ª ordem, temos que...

z ' ( x ) = 2 e 2 x - y 2 1 2

Chegando assim, ao seguinte sistema de equações...

y ' ( x ) z ' ( x ) = 0 1 c ( y ) 0 y ( x ) z ( x ) + 0 q ( x )

E então, usando o método de Euler, temos que a nossa função vai ficar assim...

f x n , y n = 2 e 2 x - y 2 1 2

f x n , y n = 2 e 2 x n - y n 2 1 2

De modo que a nossa iteração vai ser dada por...

z n + 1 = z n + 2 h e 2 x n - y n 2 1 2

Com...

z 0 = y 0 ' = 1

Passo 3

E então, fazendo nossa iterações pelo método de Euler, chegamos até os resultados da tabela abaixo...

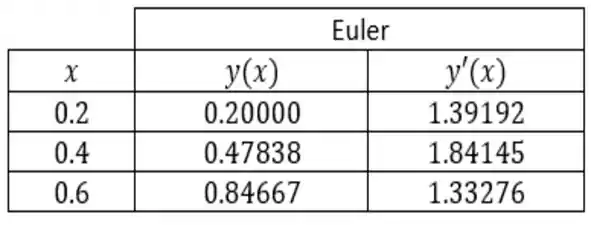
Passo 4

b) Quanto ao método de iteração do método de Euler aperfeiçoado, temos que este vai ser dado pela seguinte fórmula de iteração...

z n + 1 = z n + h 2 [ f x n , y n + f x n + 1 , y n + 1 ]

z n + 1 = z n + h 2 [ e 2 x n - y n 2 1 2 + e 2 x n + 1 - y n + 1 2 1 2 ]

Chegamos assim, aos resultados da tabela abaixo...

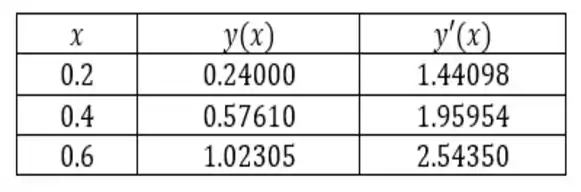
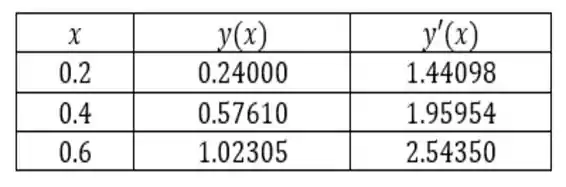
Resposta

a)

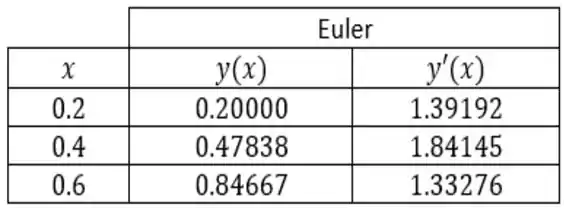
b)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize o método de Euler com d x = 0,2 para estimar y ( 1 ) se y ' = y e y 0 = 1 . Qual o valor exato de y 1 .
Utilize o método de Euler para calcular as três primeiras aproximações do problema de valor inicial dado para o tamanho do incremento especificado. Calcule a solução exata e estude a precisão de suas
Utilize o método de Euler com d x = 0,2 para estimar y ( 2 ) se y ' = y x e y 1 = 2 . Qual o valor exato de y 2 .
Use o método de Euler com o passo especificado para calcular o valor da solução no ponto dado x * . Determine o valor da solução exata em x * y ' = 2 x e x 2 , y 0 = 2 , d x = 0.1 , x * = 1
Use o método de Euler com o passo especificado para calcular o valor da solução no ponto dado x * . Determine o valor da solução exata em x * y ' = 2 y 2 ⋅ x - 1 , y 2 = - 1 2 , d x = 0.1 , x * = 3