Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 5.Exercícios - Ex. 14

14. Seja p n ( x ) o polinômio de grau ≤ n que interpola f ( x ) em x 0 , x 1 ,... x n escrito na forma de Newton.

a) Escreva um algoritmo para avaliar p n ( x - ) , x - ∈ [ x 0 , x n ] semelhante ao algoritmo dos parênteses encaixados descrito na seção 2.5.3

b) Dada a tabela

Obtenha uma aproximação para f ( 0.6 ) usando polinômio de grau 4, avaliando p 4 ( 0.6 ) através do algoritmo obtido no item (a)

Passo 1

a) O nosso algoritmo proposto é o seguinte, escrito em pseudocódigo...

P a s s o   1 :   I n í c i o   k   ←   r e t o r n a I n d i c e I n i c i a l (   g r a u ,   p t o ,   x ,   y   )  

P a s s o   2 :   t e r m o   ←   1   p   ←   y [ k ]  

P a s s o   3 :   P a r a   i   =   1   A t é   n u m P t o s   F a ç a   I n í c i o   t e r m o   ←   t e r m o   *   (   p t o   –   x [ k + i - 1 ]   )  

P a s s o   4 :   p   ←   p   +   t e r m o   *   r e t o r n a D i f e r e n c a D i v i d i d a (   k ,   i ,   x ,   y   )  

P a s s o   5 :   F i m - P a r a  

P a s s o   6 :   E s c r e v a ‘ O   v a l o r   d o   p o l i n ô m i o   n o   p o n t o   d a d o   é   ’ ,   p

P a s s o   7 :   F i m .  

Sendo que temos as seguintes variáveis pra esse nosso programa:

R e a i s : p ,   t e r m o ,   p t o ;

I n t e i r a s :   i , k , n u m P t o s ,   g r a u ;

V e t o r : x , y ;

Passo 2

b) Agora, vamos à tabela do enunciado...

Bora construir a tabela de diferenças divididas...

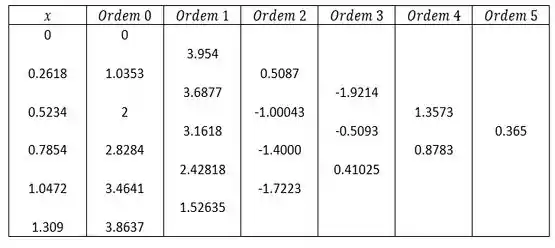
Como o que queremos é f 0.6 . Temos então que...

d 0 = 0

d 1 = 3.954

d 2 = 0.5087

d 3 = - 1.9214

d 4 = 1.3573

Chegando então, ao seguinte polinômio...

p 4 x = 3.954 x + 0.5087 x x - 0.2618 - 1.9214 x x - 0.2618 x - 0.5234 + 1.3573 x ( x - 0.2618 ) ( x - 0.5234 ) ( x - 0.7854 )

Calculando...

p 4 0.6 = 2.323

Passo 3

Utilizando Python, e de acordo com o algoritmo da letra (a), confeccionamos o seguinte código...

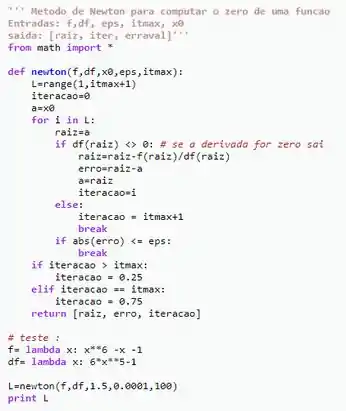
Onde obtivemos que...

f 0.6 = 2.407

Resposta

b) f 0.6 = 2.327

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um polinômio P n ( x ) , de grau n, coincide com f ( x ) = e x nos pontos 0 n , 1 n ,… , n - 1 n , n n . Qual o menor valor de n que se deve tomar a fim de que se tenha: e x - P n x ≤ 10 - 6 ,p a r a0
Sabendo-se que a equação x 4 + 6 x 2 - 1=0 tem uma raiz em [ 0,1 ] , determinar o valor aproximado dessa raiz usando polinômio de interpolação de Newton sobre 3 pontos.
Dada a tabela:a) Calcular 1,035 por meio de um polinômio de interpolação de grau adequado. b) Dar uma estimativa para o erro de truncamento.
Seja a função tabelada:a) Determinar o polinômio de interpolação de Newton; b) Calcular f ( 0.5 ) .
Considerando a função f ( x ) = x tabelada:a) Determinar o valor aproximado de 1,12 usando polinômio de interpolação de Newton sobre 3 pontos.b) Calcular um limitante superior para o erro.