Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 2.Exercícios - Ex. 2
O método da bissecção pode ser aplicado sempre que , mesmo que tenha mais que um zero em . Nos casos em que isto ocorre, verifique, com o auxílio de gráficos, se é possível determinar qual zero será obtido por este método.
Passo 1
Eai pessoal, vamos começar fazendo essa questão para a função seno!
Vamos começar com um de e um .
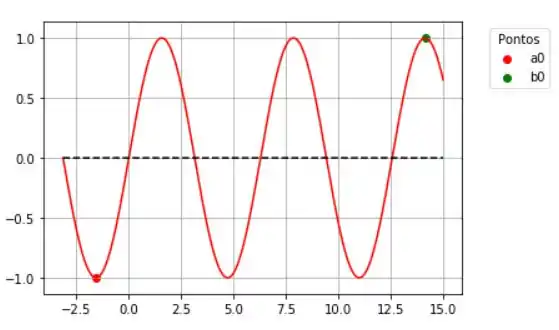
Passo 2
Agora vamos seguir o algoritmo descrito no capítulo 2 para achar o .
O algoritmo basicamente pega o ponto que tá no meio do e doe acha o valor da função nesse ponto.
Ou seja:
O vai substituir o ponto em que o valor de tenha o mesmo sinal entre { e }
Vamos ver na prática que fica mais fácil!
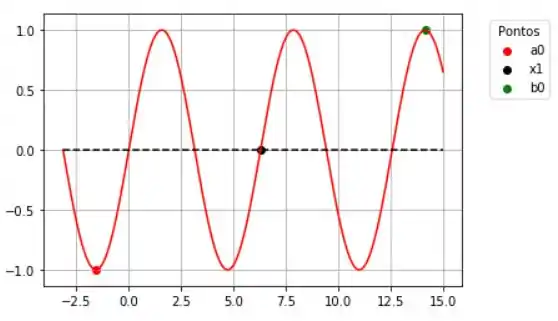
Aqui a gente pode ver que o ponto é zero, sabendo disso, esse já é o resultado final do algoritmo e não precisamos mais fazer nada!
Já dá pra ver que a primeira raíz foi pulada, disso a gente já pode inferir que é impossível determinar a ordem das raízes a partir do método da bissecção.
Resposta
é impossível determinar a ordem das raízes a partir do método da bissecção.