Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Exercícios complementares - Ex. 31a

Aplique o método da bissecção para resolver:

a)

Obtendo em cada caso a e b (iniciais) graficamente.

Passo 1

Eaí! Tudo na paz? Vamos mais uma vez usar o método da bissecção para resolver o exercício. Como vamos ter que pegar os valores iniciais do intervalo graficamente, não vamos precisar provar que existe raiz, já que o gráfico vai deixar isso evidente quando cortar o eixo x em algum ponto. Pega aí sua calculadora gráfica e bora lá.

Passo 2

Analisando o gráfico:

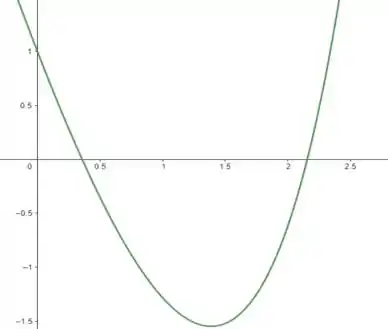
Vemos que o eixo x é cortado duas vezes, logo temos duas raízes presentes nos intervalos .

Verificando os sinais:

Aplicando o método da bissecção vamos obter:

Novo intervalo (substituindo pelo 0.5):

Limitando o intervalo novamente:

Continuando as iterações, o valor encontrado será aproximadamente .

Passo 3

Aplicando o método para achar a raiz no intervalo iremos obter aproximadamente o valor de , basta seguir o que foi feito no passo dois, lembre-se de considerar que:

Para realizar a substituição dos intervalos. Para o primeiro intervalo, por exemplo, teríamos:

E seu valor aplicado na função:

E como o resultado foi negativo, teríamos que substituir 2 por 2.125 ficando com .

Resposta

Exercícios de Livros Relacionados

Pelo Teorema do Valor Médio temos que x k + 1 - ξ = φ ' ( c k ) ( x k - ξ ) com c k entre x k e ξ . Analise os sinais de x j - ξ , j = 0,1 , . . .

O método da bissecção pode ser aplicado sempre que f ( a ) f ( b )0 , mesmo que f ( x ) tenha mais que um zero em ( a ,b ) . Nos casos em que isto ocorre, verifique, com o auxílio de gráficos, se é po

Aplique o método da bisseção e regula falsi para calcular a raiz positiva de 𝑥 2 − 7 = 0 com 𝑒 10 − 2 , partindo do intervalo inicial 2.0 , 3.0 .

Aplique o método da bissecção para resolver:b) 𝑥 3 + c o s c o s𝑥= 0 Obtendo em cada caso a e b (iniciais) graficamente.

O problema: resolva 𝑓 𝑥 = 𝑥 + l n l n𝑥= 0 pode ser transformado num problema equivalente da forma 𝑥 = Ψ 𝑥 . Para o processo iterativo definido por 𝑥 𝑘 + 1 = Ψ 𝑥 ; Analisar a c