Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 5.Exercícios - Ex. 4

Dados:

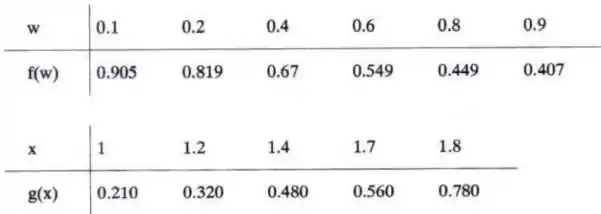
Calcule o valor aproximado de x tal que f(g(x)) = 0.6, usando polinômios interpolantes de grau 2.

Passo 1

Então pessoal, essa daqui é mais complicada, mas dá pra resolver!

Passo 2

Primeiro, vamos interpolar f ( w ) , usando os pontos 0.4 ,   0.6 e 0.8 , que são os mais próximos de f w = 0.6 , ok? Assim, por interpolação usando sistema linear:

p 2 w = a 0 + a 1 w + a 2 w 2

Substituindo os pontos:

p 2 0.4 = a 0 + a 1 0.4 + a 2 0.4 2 = 0.67

p 2 0 . 6 = a 0 + a 1 0 . 6 + a 2 0 . 6 2 = 0 . 549

p 2 0 . 8 = a 0 + a 1 0 . 8 + a 2 0 . 8 2 = 0 . 449

Podemos montar esse sisteminha aqui:

1 0.4 0.16 1 0.6 0.36 1 0.8 0.64 a 0 a 1 a 2 = 0.67 0.549 0.449

Na forma aumentada:

1 0.4 0.16 1 0.6 0.36 1 0.8 0.64 0.67 0.549 0.449

Resolvendo esse sistema pela eliminação de Gauss, chegamos no resultado:

a 0 = 0.975

a 1 = - 0.8675

a 2 = 0.2625

Assim:

p 2 w = 0.975 - 0.8675 w + 0.2625 w 2

Se queremos que p w = 0.6 :

0.975 - 0.8675 w + 0.2625 w 2 = 0,6

0 . 375 - 0.8675 w + 0.2625 w 2 = 0

Assim:

w 1 = 2.7933

w 2 = 0.5114

Hmmm, mas qual valor está certo? Repare que se f w = 0.6 , w deve estar entre 0.4 e 0.6 , pela tabela, certo? Então, nosso valor será w = 0.5114 .

Passo 3

Agora, vamos reparar que se temos f g x , nossa g ( x ) está assumindo o papel de w , certo?? Logo, para descobrir o valor de x , para que f g x = 0.6 , devemos saber o valor de x para que g x = w = 0.5114 , como vimos no passo anterior!

Para isso, vamos interpolar g ( x ) da mesma forma que fizemos para f ( w ) , beleza?? Vamos lá! Se queremos g x = 0.5114 , vamos pegar os pontos 1.2 , 1.4 e 1.7 para achar o polinômio por interpolação quadrática. Assim:

p 2 x = a 0 + a 1 x + a 2 x 2

Substituindo os pontos:

p 2 1.2 = a 0 + a 1 1.2 + a 2 1.2 2 = 0 . 32

p 2 1.4 = a 0 + a 1 1.4 + a 2 1.4 2 = 0 . 48

p 2 1.7 = a 0 + a 1 1.7 + a 2 1.7 2 = 0 . 56

Podemos montar esse sisteminha aqui:

1 1.2 1.44 1 1.4 1.96 1 1.7 2.89 a 0 a 1 a 2 = 0 . 32 0 . 48 0 . 56

Na forma aumentada:

1 1.2 1.44 1 1.4 1.96 1 1.7 2.89 0.32 0.48 0.56

Resolvendo esse sistema pela eliminação de Gauss, chegamos no resultado:

a 0 = - 2.432

a 1 = 3.5733

a 2 = - 1.0667

Assim:

p 2 x = - 2.432 + 3.5733 x - 1.0667 x 2

Se queremos que p x = 0.5114 :

- 2.432 + 3.5733 x - 1.0667 x 2 = 0.5114

- 2.9434 + 3.5733 x - 1.0667 x 2 = 0

Assim:

x 1 = 1.4603

x 2 = 1.8895

Hmmm, vamos nos perguntar a mesma coisa que no passo anterior: mas qual valor está certo? Repare que se g x = 0 . 5114 , x deve estar entre 1 . 4 e 1 . 7 , pela tabela, certo? Então, nosso valor será x = 1.4603 .

Essa é a nossa resposta! 😊 Pois esse é o valor de x em que f g x = 0.6 .

Resposta

x = 1.4603

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Queremos construir uma tabela que contenha valores de cos(x) para pontos igualmente espaçados no intervalo I = [l, 2]. Qual deve ser o menor número de pontos desta tabela para se obter, a partir dela,
Resolva o exercício proposto na introdução deste capítulo. Verifique que um polinômio de grau 2 é uma boa escolha para obter f(32.5); use um processo de interpolação linear para obter o ponto x para o
Dada a tabela abaixo, Calcule e3· 1 usando um polinômio de interpolação sobre três pontos. Dê um limitante para o erro cometido.
Construa uma tabela para a função f(x) = cos(x) usando os pontos: 0.8, 0.9, 1.0, 1.1, 1.2 e 1.3. Obtenha um polinômio de grau 3 para estimar cos(l.07) e forneça um limitante superior para o erro.