Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 6.Exercícios - Ex. 4

A tabela abaixo mostra as alturas e pesos de uma amostra de nove homens entre as idades de 25 a 29 anos, extraída ao acaso entre funcionários de uma grande indústria:

  1. Faça o diagrama de dispersão dos dados e observe que parece existir uma relação linear entre a altura e o peso.
  2. Ajuste uma reta que descreva o comportamento do peso em função da altura, isto é, p e s o = f a l t u r a .
  3. Estime o peso de um funcionário com 175 cm de altura, e estime a altura de um funcionário com 80kg.
  4. Ajuste agora a reta que descreve o comportamento da altura em função do peso, isto é, a l t u r a = g ( p e s o ) .
  5. Resolva o item c com essa nova função e compare os resultados obtidos. Tente encontrar uma explicação.
  6. Coloque num gráfico as equações b e d e compare-as.

Passo 1

Fala galerinha, tudo certinho?

Bom, esse exercício é para aplicarmos a ferramenta do método dos mínimos quadrados.

Olhando o gráfico de dispersão da função:

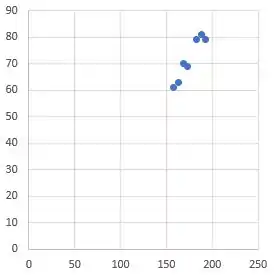
Perceba que o comportamento do gráfico se comporta de maneira linear.

Quando fizermos a aproximação linear, teremos:

φ x k = a 0 + a 1 x k

E para isso usaremos:

a 0 m + a 1 ∑ k = 1 m x k = ∑ k = 1 m y k

E também:

a 0 ∑ k = 1 m x k + a 1 ∑ k = 1 m x k 2 = ∑ k = 1 m x k y k

Onde teremos:

a 0 = ∑ k = 1 m x k 2 ∑ k = 1 m y k - ∑ k = 1 m x k y k ∑ k = 1 m x k m ∑ k = 1 m x k 2 - a ∑ k = 1 m x k 2

a 1 = m ∑ k = 1 m x k y k - ∑ k = 1 m y k ∑ k = 1 m x k m ∑ k = 1 m x k 2 - a ∑ k = 1 m x k 2

Passo 2

Para calcular e equação linear, precisaremos calcular alguns termos como: x k ,   y k ,   x k 2 e x k y k e o somatório de cada um dos termos.

Uma coisa que iremos fazer aqui para facilitar os nossos cálculos é fazer essa regressão na calculadora. Onde você aperta MODE+REG+LOG. Aí você vai inserir os dados você aperta SHIFT+1 onde a calculadora te dá o somatório de: x 2 ,   x ,   y , x y .

Onde teremos:

A calculadora também nos fornece a equação linera com A e B (aperte SHIFT+2, role até chegar em A e B):

y = 0,52757 x - 20,078

Convertendo para metros:

y = 52,76 x - 20,078

Passo 3

Substituindo na fórmula encontrada, um cara com 1,75m ( x = 1,75 ), teremos:

y = 52,76 . 1,75 - 20,078

y = 72,2467   k g

O primeiro conjunto de pontos é ( 1.75 ;   72.2467 ) .

A altura de alguém com 80kg pode ser dada:

80 = 52,76 x - 20,078

x = 1,89 m

O segundo conjunto de pontos será ( 1.89 ; 80 )

Resposta

y = 52,76 x - 20,078

( 1.75 ;   72.2467 )

( 1.89 ; 80 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f x = 1 x + 2 ,x ∈ [ - 1,1 ] . Usando o método dos mínimos quadrados, aproximar a função f ( x ) por um polinômio do 2 ° grau.
Usando o método dos mínimos quadrados, aproximar a função f x = x 3 - 1 2 ,x ∈ [ 0,1 ] a) por uma reta;b) por um polinômio do 2 ° grau.
Considere a função f ( x ) , dada por:Onde x k = 2 k π 12 . Obtenha aproximação trigonométrica, de ordem 2, usando o método dos mínimos quadrados.
Determinar, pelo método dos mínimos quadrados, a reta mais próxima dos pontos ( x i, y i ) para a função y=f ( x ) tabelada:
Aproximar, pelo método dos mínimos quadrados, a função f ( x )=x 3+4x , no intervalo [ 0,1 ] , a) por uma reta;b) por um polinômio do 2° grau.