Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Exercícios - Ex. 27
Verifique que não é possível determinar as raízes de , utilizando o algoritmo Q-D
Passo 1
Opa galerinha aqui quem fala é a jacyara e hoje vamos resolver mais uma questãozinha de cálculo numérico.
A questão te informa que não é possível encontrar as raízes do polinômio pelo algoritmo Q-D e pede para você mostrar isso.
Bem, o Algoritmo Q-D é um método para encontrar raízes de polinômios baseado na construção de uma tabelinha.
Que dado um polinômio do tipo:
Podemos construir uma tabelinha que as primeiras duas linhas podem ser dada da seguinte forma:
E os novos e podem ser calculados com as seguintes expressões:
Onde varia de até o grau máximo do polinômio portanto, como temos um polinômio de grau temos apenas até e temos que .
E para provar o que a alternativa pede temos que provar que ao longo da conta para montagem dessa matriz existe algum , porque mostra uma divisão por mostrando que o método não pode ser utilizado.
Mas e ai? Podemos começar? Vamos lá.
Passo 2
Primeiramente, vamos analisar o nosso polinômio que é dado por:
Portanto, temos que nossos coeficientes são dados por:
Agora vamos montar a primeira linha da nossa tabelinha fazendo .
Agora vamos utilizar as formulas de recorrência para calcular os novos e gerar a seguinte tabelinha:
E vamos agora calcular os novos e gera mais uma linha na nossa tabelinha:
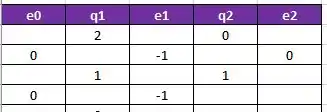
Agora vamos calcular nosso novo , mas olha só:
Como temos um o método não pode continuar e não pode encontrar as raízes da equação.
Resposta
Ei, a resposta está no passo a passo :)