Um dispositivo tem uma certa característica y que ´e função de uma variável x . Através de várias experiências foi obtido o gráfico:Deseja-se conhecer o valor de y para x=0 , 5 . Da teoria sabe-se que a função que descreve y tem a forma aproximada de uma curva do tipo a x 2+bx . Obtenha valores aproximados para aeb , usando todas as observações, e então estime o valor para y quando x= 0 , 5 .

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 8.Exercícios complementares - Ex. 22

Um dispositivo tem uma certa característica que ´e função de uma variável . Através de várias experiências foi obtido o gráfico:

Deseja-se conhecer o valor de para . Da teoria sabe-se que a função que descreve tem a forma aproximada de uma curva do tipo a . Obtenha valores aproximados para , usando todas as observações, e então estime o valor para quando .

Passo 1

Falaaaaa rapaziada tudo blz?

Nessa questão do livro de cálculo numérico de Franco e Neide Um dispositivo tem uma certa característica que ´e função de uma variável . Através de várias experiências foi obtido o gráfico:

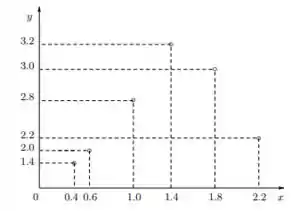
Deseja-se conhecer o valor de para . Da teoria sabe-se que a função que descreve tem a forma aproximada de uma curva do tipo a . Obtenha valores aproximados para , usando todas as observações, e então estime o valor para quando .

Precisa ficar assim não meus abençoados conforme você for vendo os passos vai perceber que ela é de boa.

Passo 2

Então galera para estimar o valor de para , analisando o gráfico no passo anterior temos que para,

Ficando para,

O valor de,

Ficando,

Chegando em,

Espero que eu tenha ajudado e te vejo no próximo desafio.

Até a próxima.

Resposta

Exercícios de Livros Relacionados

7. O número de bactérias por unidade de volume, existente em uma cultura após x horas é apresentado na tabela:a) Verifique que uma curva para se ajustar ao diagrama é do tipo exponencialb) ajuste aos

12. Considere a tabela...Deseja-se aproximar a função y ( x ) tabelada nos pontos distintos ( x i , y i ) para i = 1 , … , m . Podemos fazer a regressão linear de y por x obtendo y = a x + b . Podemos

Determinar a parábola mais próxima dos pontos ( x i, y i ) para a função y=f ( x ) tabelada:

Seja f x = 1 x 4 ,x ∈ 0,1 . Usando o método dos mínimos quadrados, aproximar a função f(x) por um polinômio do tipo P x = a x 2 + b x 4 , usando o seguinte produto escalar: f , g = ∫ 0 1 x 2f xg xd x{

Usando o método dos mínimos quadrados, aproximar a função f x = x 2 - 3 x + 4 2 ,x ∈ 0,1 ; a) por uma reta;b) por um polinômio do 2° grau.