Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Problemas Aplicados e Projetos - Ex. 6
A equação:
Permite calcular o ângulo de inclinação, , em que o lançamento do míssil deve ser feito para atingir um determinado alvo. Na equação acima,
- -ângulo de inclinação com superfície da terra com a qual é feita o lançamento do míssil
- – Aceleração da gravidade
- − Raio da terra
- – Velocidade do lançamento do míssil, ,
- – ângulo (medido do centro da terra) entre o ponto de lançamento e o ponto de impacto desejado.
Resolva o problema considerando: e tal que , ou seja, aproximadamente .
Passo 1
E aí galera do Responde Ai, quem fala aqui é a Jacyara e estamos aqui para resolver uma questãozinha de cálculo numérico.
A questão te fornece um bocado de informação em relação ao lançamento de um míssil e te informa essa equaçãozona aqui que relaciona todas as variáveis do lançamento:
Além disso te dá as seguintes informações:
e
E te pergunta a seguinte informação quem é ?
Só que aqui você não consegue isolar o em função das demais variáveis e considera-se que isso aqui é uma equação não linear.
Só que para resolver esse tipo de questão que envolve encontrar raízes de soluções para equações não lineares, precisamos utilizar um método iterativo, o método iterativo é um método que possui uma sequência de passos que se repetem, até que a solução seja alcançada com a tolerância fornecida e o método que vamos utilizar é o método de newton por ele precisar apenas de uma única estimativa e ter uma convergência mais acelerada.
Eu não sou muito amigável com a ideia de decorar as coisas, mas sugiro que em cálculo numérico decore os passos dos métodos porque é uma ajuda imensa na resolução das questões. Enfim, o método de newton para equações não lineares é o seguinte:
- Primeiro passo: estimativa inicial.
- Segundo passo: Calcular o valor do sistema com a estimativa inicial.
- Terceiro passo: verificar a convergência.
- Quarto passo: Método de Newton – cálculo da derivada
- Quinto passo: Calcular o incremento e a estimativa atualizada.
- Sexto passo: Repetir os passos anteriores até atingir a convergência.
Como a questão não definiu o critério de convergência, vamos definir um valor de por ser um valor pequeno e se aproximar do 0 e já é um valor de bom tamanho, valores menores do que esse podem gerar passos demasiados.
Agora que temos o roteiro, vamos na prática ver como isso funciona. E aí? Podemos ir? Vamos lá.
Passo 2
Primeiramente, precisamos da equação não linear e essa equação nos é informada na nossa questãozinha.
Substituindo os valores fornecidos pela questão na nossa equação temos que:
Calculando a derivada para o método de newton temos:
Utilizando a seguinte expressão, temos:
E derivando a equação temos que:
Agora que temos as funções a derivada da , precisamos aplicar o método de newton em cada equação e encontrar a raiz de cada equação.
Mas antes de tudo, vamos fazer uma estimativa né? Como encontrar essa estimativa?
A melhor maneira é plotar a função, eu plotei fazendo variar até e encontrei o seguinte gráfico:
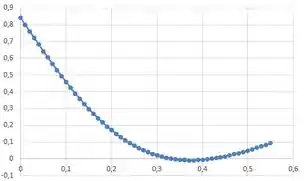
Analisando o nosso gráfico, podemos verificar que temos uma raiz próximo de então essa vai ser nossa estimativa inicial.
Agora vamos utilizar o método de newton, belezinha? Vamos lá
Passo 3
Vamos procurar a raiz da primeira equação que a raiz de:
E para resolver a questão vamos utilizar o método que foi apresentado no passo 1, vamos chutar uma estimativa inicial , portanto temos que:
- Primeiro passo:
- Segundo passo:
- Terceiro Passo: , portanto não é raiz
- Método de Newton – Cálculo da derivada:
- Método de Newton – incremento da solução:
Como não encontramos a raiz ainda, sendo assim, precisamos aplicar o método de newton até que o valor da função seja menor que a tolerância, portanto:
- Primeiro passo:
- Segundo passo:
- Terceiro Passo: , portanto é a raiz.
Essa foi rapidinho né?
Mas e aí?
Curtiu? Responde Ai, vlwwwwwws e até a próxima.