Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Problemas Aplicados e Projetos - Ex. 8
Uma loja de eletrodomésticos oferece dois planos de financiamento para um produto cujo o preço à vista é
- Plano A: entrada de + prestações iguais de
- Plano B: entrada de + 12 prestações iguais de
Qual dos dois planos apresenta a menor taxa de juros, sendo, portanto, melhor para o consumidor?
Observação: Sabe-se que a equação relaciona juros () e o prazo com o valor financia e a prestação mensal é dada por:
- Fazendo e , verificar que a equação anterior se transforma em:
- Escrever a equação anterior para o problema proposto e encontrar um intervalo encontrando a solução positiva, diferente de .
Passo 1
E aí galera do Responde Aí, aqui quem fala é a jacyara e hoje vamos resolver mais uma questãozinha de cálculo numérico.
Bem, a questão te fornece um bocado de informação e te faz algumas perguntas em relação à informação.
A questão te pergunta primeiramente qual é o melhor plano oferecido, após isso temos duas alternativas.
A alternativa a) te pergunta se caso eu pegar essa equação:
E faço as seguintes observações:
É possível chegar na seguinte equação:
E a segunda alternativa é encontrar os valores das soluções positivas dessa equação acima.
Bem, para responder qual plano é o melhor eu preciso saber qual deles possui a menor taxa de juros.
Portanto, temos que responder primeiramente a alternativa a) e b), porque o dá uma medida direta da taxa de juros do plano, portanto, o plano que tiver o menor valor de apresenta o melhor plano.
Para encontrar o valor de que te fornece a igualdade na equação como a questão não explicita nenhum método, podemos utilizar apenas uma representação gráfica da função.
E ai? Podemos começar? Vamos nessa então.
Passo 2
Para responder a alternativa a) vamos partir da equação geral:
Substituindo as seguintes informações na questão:
Temos que:
Portanto, temos que:
Realizando operações matemática temos:
Realizando mmc, temos:
Portanto, temos que não pode ser 0, portanto:
E aí, vamos para a alternativa b) ? vamos lá.
Passo 3
Para resolver a alternativa b) vamos saber qual é o melhor plano em paralelo.
Primeiramente vamos calcular o valor de e de para cada plano, belezinha?
Vamos lá.
Como é o número de prestações, temos que:
Como foi informado na questão, consequentemente temos uma formulinha para calcular o valor do que também é fornecido pela questão, portanto temos:
Gerando as seguintes equações
Para o plano a)
No caso do plano b)
Plotando ambas as curvas, temos os seguintes gráficos:
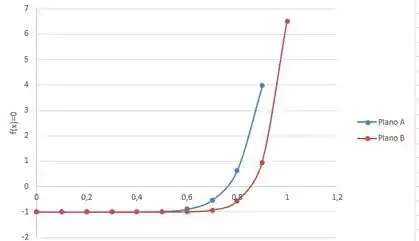
Como temos que o zero da função do plano A ocorre com um menor, a sua taxa de juros é menor, portanto, o Plano A é melhor.
Em relação aos intervalos para responder a alternativa , olhando o gráfico temos que a solução de ambos os planos se localiza no intervalo entre 0,6 até 0,9.
E aí sacou? Entendeu tudinho? Responde Ai e vlwwwwws
Resposta
Todas os passos foram devidamente demonstrados no passo anterior.