Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 2.Exercícios - Ex. 1
Localize graficamente as raízes das equações a seguir:
Passo 1
Letra a:
Então galera vamo lá..
Existem 3 formas de fazer isso, da pra ver as três formas na página 33 da segunda edição do livro.
A gente vai escolher aqui a II.
Primeiro, sabemos que se
então:
O método II diz que pra achar essas raízes, a gente só precisa plotar:
e comparar o lugar em que os gráficos se encontram!
Então:
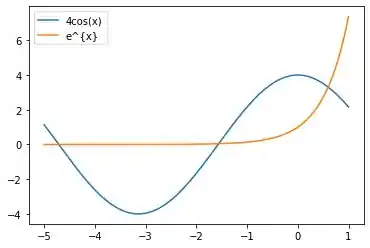
Nesse caso, existirão infinitas raízes negativas de:
Isso se dá por conta da pelo comportamento periódico da função cosseno, junto com o fato da função exponencial tender a zero no infinito.
Essas raízes negativas vão estar nos intervalos definidos pelos valores próximos de zero da função cosseno, que são periódicos, logo as raízes vão estar num intervalo:
Já que a função exponencial explode para infinito de forma sempre crescente quando x é positivo, podemos perceber que só vai ter uma raiz positiva dessa , que vai estar no intervalo
Passo 2
Letra b:
Então galera vamo lá..
Existem 3 formas de fazer isso, da pra ver as três formas na página 33 da segunda edição do livro.
A gente vai escolher aqui a II.
Primeiro, sabemos que se
então:
O método II diz que pra achar essas raízes, a gente só precisa plotar:
e comparar o lugar em que os gráficos se encontram!
Então:
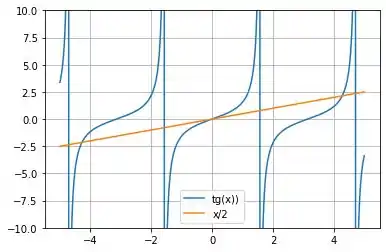
Nesse caso, existirão infinitas raízes de:
Isso se dá por conta da pelo comportamento periódico da função tangente, junto com o fato dela atingir valores que vão de , a cada ciclo periódico.
Essas raízes vão estar nos intervalos definidos pelos valores que explodem da função tangente, que são periódicos, logo as raízes vão estar num intervalo:
Além disso, facilmente podemos verificar que e , logo 0 é uma raíz também!
Passo 3
Letra c:
Então galera vamo lá..
Existem 3 formas de fazer isso, da pra ver as três formas na página 33 da segunda ediç��o do livro.
A gente vai escolher aqui a II.
Primeiro, sabemos que se
então:
O método II diz que pra achar essas raízes, a gente só precisa plotar:
e comparar o lugar em que os gráficos se encontram!
Então:
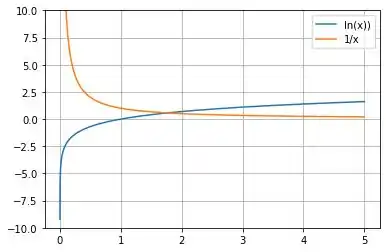
Nesse caso, existirá apenas uma única raíz, já que a função só cresce e a função decresce!
Podemos observar também que esse ponto de encontro está entre [1,2].
Passo 4
Letra d:
Então galera vamo lá..
Existem 3 formas de fazer isso, da pra ver as três formas na página 33 da segunda edição do livro.
A gente vai escolher aqui a II.
Primeiro, sabemos que se
então:
O método II diz que pra achar essas raízes, a gente só precisa plotar:
e comparar o lugar em que os gráficos se encontram!
Então:
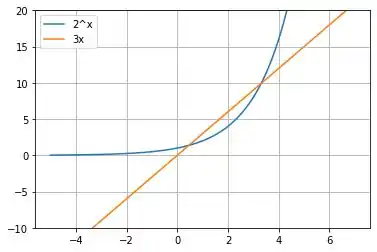
Nesse caso, existirá duas raízes, já que a função só cresce e de forma maior que a função !
Podemos observar também que esse primeiro ponto de encontro está entre [0,1].
Já o segundo ponto, podemos ver pelo gráfico que fica entre .
Passo 5
Então galera vamo lá..
Existem 3 formas de fazer isso, da pra ver as três formas na página 33 da segunda edição do livro.
A gente vai escolher aqui a II.
Primeiro, sabemos que se
então:
O método II diz que pra achar essas raízes, a gente só precisa plotar:
e comparar o lugar em que os gráficos se encontram!
Então:
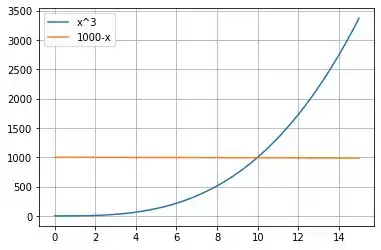
Nesse caso podemos considerar como uma constante e calcular da seguinte forma.
para ser mais correto, podemos dizer que a raíz vai estar
Resposta
- Uma raiz positiva no intervalo .
- e infinitas raízes nos intervalos:
- Uma raíz entre
- Uma raíz entre
- Uma raíz entre
Infinitas raízes negativas nos intervalos