Seja
- Encontre os valores positivos de para que tenha apenas uma raiz estritamente positiva.
- Encontre os valores positivos de para que tenha três raízes estritamente positivas.
Passo 1
Vamos analisar os casos em que
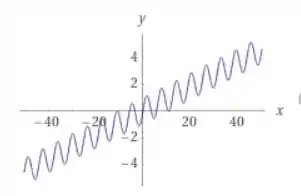
Para essa função ter apenas uma raiz positiva, temos que ter apenas uma raiz em .
Aqui fica o gráfico para esse valor:
Passo 2
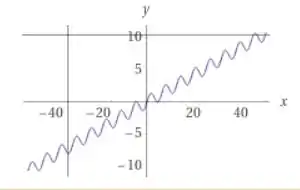
Na letra b, temos que ter 3 raízes, então
Aqui fica o gráfico para esse valor: