Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 1.Exercícios complementares - Ex. 43
Mostre que uma matriz e sua transposta possuem o mesmo polinômio característico.
Passo 1
Eaiiii!!! Bora para mais um exerciciozinho! Vamos lembrar que a equação para determinar o polinômio característico é :
Passo 2
Sabemos que:
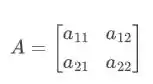
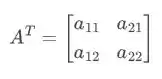
Para que possuam o mesmo polinômio característico, as matrizes devem ser simétricas.
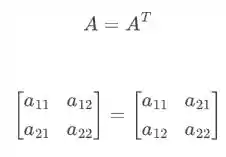
Como as mesmas são simétricas, podemos concluir que possuem o mesmo polinômio característico.
Resposta
Possuem o mesmo polinômio característico por serem simétricas.
Exercícios de Livros Relacionados
Em relação ao produto escalar usual do R 3 , calcule ( x , y ) nos seguintes casos: a) x = 1 2 ,2 ,1 t , y = 4 ,1 ,- 3 t ;b) x = 2 ,1 ,0 t , y = 4 ,0 ,2 t ;
Seja B 1 = 5 , x - 1 , x 2 - 3 x eB 2 = { 8 ,3 x + 2,5 x 2 - 3 x } bases de k 2 x . Seja P 2 x = 8 5 + 4 x - 1 + 3 { x 2 - 3 x } . Calcular as coordenadas de P 2 ( x ) em relação à base B 2 .
Sejam x = x 1 , x 2 t e y = y 1 , y 2 t dois vetores quaisquer do R 2 . Mostre que: x , y = x 1 x 2 a 2 + y 1 y 2 b 2 Com a ,b ∈ R fixos e não nulos define um produto escalar sobre R 2 .
No espaço vetorial R 4 , munido do produto escalar usual, sejam x = 1 ,2 ,0 ,1 t e y = 3 ,1 ,4 ,2 t . Determine: x , y ,x ,y ,d x , ye x + y | | x + y | |
Seja v = 3 b_1 + 4 b_2 + 2 b_3 , onde:b_1 = (1,1 , 0)^t ; b_2 = (- 1,1 , 0)^t ; b_3 = (0,1 , 1)^t Com s coordenadas de v na base:f_1 = (1,1 , 1)^t ; f_2 = (1,1 , 0)^t ; f_3 = (1,0 , 0)^t