Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 2.Exercícios - Ex. 4
Seja que possui um zero no intervalo
Se o objetivo for obter uma aproximação para esta raiz de tal forma que é aconselhável usar o método da posição falsa tomando como intervalo inicial? Justifique gráfica e analiticamente sem efetuar iterações numéricas.
Cite outros métodos nos quais esse objetivo possa ser atingido.
Passo 1
Então pessoal, vamos começar fazendo apenas iterações geométricas.
Se fizermos o gráfico de , após a primeira iteração vamos ter isso daqui:
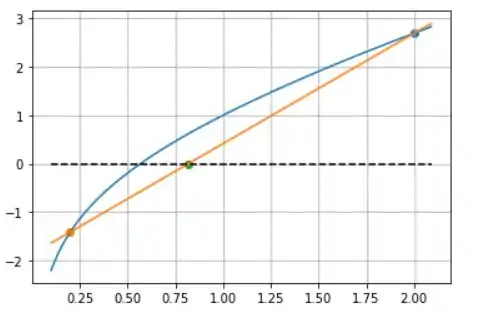
Passo 2
Na segunda iteração, teremos:
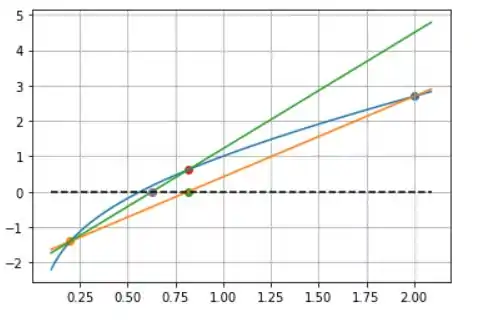
Daqui podemos observar que o limite inferior sempre ficará parado, enquanto que o limite superior vai variar, ou seja, a sequência gerada não vai oscilar em torno da raiz!
Então, a única possibilidade disso daqui dar certo é se , já que não podemos garantir que essa sequência vai convergir.
Como então essa sequência não vai convergir!
Passo 3
Como , e a função é contínua dentro do intervalo , podemos utilizar o método da bissecção e o método de Newton-Raphson, já que a é derivável, e sua derivada é contínua , além da derivada não assumir valores nulos dentro do intervalo de análise.
Resposta
Como então essa sequência não vai convergir!
Como , e a função é contínua dentro do intervalo , podemos utilizar o método da bissecção e o método de Newton-Raphson, já que a é derivável, e sua derivada é contínua , além da derivada não assumir valores nulos dentro do intervalo de análise.