Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 3.Problemas Aplicados e Projetos - Ex. 11

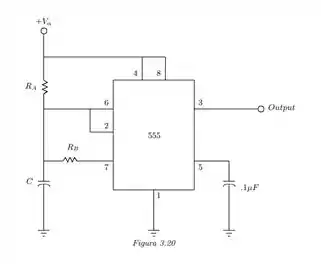
Suponha que tenhamos um circuito temporizador 555 dado como mostra a figura 3.20

Cuja a onda de saída é da forma:

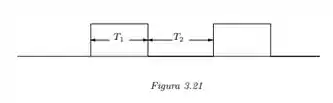
Com

T 1 + T 2 = 1 f

Onde f é a frequência, e o ciclo de trabalho C T é dado por:

C T = T 1 T 2 + T 1 * 100 %

Pode-se mostrar que:

T 1 = R a ∙ C ∙ L n 2

T 2 = - R a R b C R a + R b ∙ l n l n   R a - 2 R b - 2 R a - R b  

Dado que R a = 8.670 , C = 10 - 7 , T 2 = 14 * 10 - 5 ,   determine R b , T 1 , f e o ciclo de trabalho C T .

Passo 1

E aí galera do Responde Aí, aqui quem fala é a Jacyara e hoje vamos resolver mais uma questãozinha de cálculo numérico.

A questão te fornece um bocado de informação, porém, em síntese a questão pede para você calcular os valores de R b , T 1 , f e C T .

Felizmente, a questão te dá todos os dados possíveis para realizar esses cálculos e então se torna uma questão de aplicação de fórmula que também foi fornecida pela questão, beleza?

Primeiramente, vamos calcular T 1 através dessa formulinha:

T 1 = R a ∙ C ∙ L n 2

Porque todos os demais dados já foram fornecidos, agora vamos calcular o f e o C T porque o valor de T 2 já foi fornecido na questão e vamos fazer isso utilizando as seguintes formulas:

C T = T 1 T 2 + T 1 * 100 %

T 1 + T 2 = 1 f

Agora só falta calcular o valor de R b que pode ser calculado através da seguinte equação:

T 2 = - R a R b C R a + R b ∙ l n l n   R a - 2 R b 2 R a - R b  

Só que aqui temos um probleminha, essa é uma equação não linear e, portanto, precisamos de um método não linear.

Vamos utilizar o método de newton pois, detém uma convergência mais rápida.

Eu detesto decorar as coisas, mas aqui aconselho decorar o roteiro para obter essas soluções.

A equação que queremos resolver é encontrar um valor de R b tal que:

F = T 2 + R a R b C R a + R b ∙ l n l n   R a - 2 R b 2 R a - R b   = 0

E para encontrar esse valor, vamos utilizar o seguinte passo a passo:

  1. Primeiro passo: estimativa inicial.
  2. Segundo passo: Calcular o valor do sistema com a estimativa inicial.
  3. Terceiro passo: verificar a convergência.

    1. F 1 ≤ 1 E - 3

  4. Quarto passo: Método de Newton – cálculo da derivada F ' ( x )

  5. Quinto passo: Calcular o incremento e a estimativa atualizada.

    1. x = x + F ( x ) F ' ( x )

  6. Sexto passo: Repetir os passos anteriores até atingir a convergência.

Como a questão não definiu o critério de convergência, vamos definir um valor de 1 E - 2 por ser um valor pequeno e se aproximar do 0 e já é um valor de bom tamanho, valores menores do que esse pode gerar passos demasiados.

Agora que temos o roteiro, vamos na prática ver como isso funciona. E aí? Podemos ir? Vamos lá.

Passo 2

Primeiramente vamos calcular as demais coisas por ser mais simples, belezinha? Vamos lá

Para o cálculo do T 1 vamos utilizar a seguinte formulinha:

T 1 = R a ∙ C ∙ L n 2

Utilizando os dados da questão, temos:

T 1 = 8.670 * 10 - 7 * L n 2 ≅ 6 * 10 - 7

Agora vamos calcular a frequência que é dada por:

T 1 + T 2 = 1 f

Sendo assim:

6 * 10 - 7 + 14 * 10 - 5 = 14,06 * 10 - 5 = 1 f

E o ciclo de trabalho é dado por:

C T = T 1 T 2 + T 1 * 100 %

Portanto:

C T = 6 * 10 - 7 14,06 * 10 - 5 * 100 % = 0,42 %

Agora precisamos calcular o valor R b e para isso vamos precisar do valor da derivada de T 2 em função de R b , sendo assim:

∂ T 2 ∂ R b = C * R a * R a * l n l n   R a - 2 R b 2 R a - R b   R a + R b 2 - 3 * R a * R b ( R a - 2 R b ) ( 2 R a - R b ) ( R a + R b )

E consequentemente temos que:

F = T 2 + R a R b C R a + R b ∙ l n l n   R a - 2 R b 2 R a - R b   = 0

Agora que temos todos os dados vamos aplicar o método de newton para encontrar o valor do R b .

Passo 3

O tempo T 2 é uma medida positiva e, portanto, temos que o logaritmo precisa ser negativo para quando a função some com T 2 e seja 0 como mostrado na equação abaixo.

F = T 2 + R a R b C R a + R b ∙ l n l n   R a - 2 R b 2 R a - R b   = 0

Sendo assim, para o logaritimo ser negativo, temos que:

0 < R a - 2 R b 2 R a - R b < 1

Portanto, temos que R b < R a 2 , e devido a isso vamos utilizar R a 4 como nossa estimativa inicial.

Sendo assim, temos que R a 4 ≅ 2,5

Aplicando o método de newton temos:

  1. Estimativa inicial: x = 2,5
  2. Segundo passo: F x = 0,0014
  3. Terceiro passo: 0,00014 < 10 - 3 e temos que R b ≅ 2,5 é uma raiz para uma aproximação de 10 - 3 .

Passo 4

Todas as etapas foram devidamente discutidas nos passos anteriores.

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Considere a equação 𝑥 − 5 𝑒 − 𝑥 = 0 . Obtenha a raiz positiva com quatro casas decimais corretas. Confirme que a ordem de convergência do método das secantes é 𝑝 ≈ 1.6818   .
Determinar todas as raízes do polinômio: 𝑃 𝑥 = 𝑥 3 − 5 𝑥 2 − 𝑥 + 5 = 0 , com precisão de 10 − 2 , usando o método de Newton e o algoritmo de Briot-Ruffini-Horner para o cálculo da primeira raiz.
Usando o método de Newton determine, sem efetuar divisão, o valor numérico de 𝑥 = 1 3 com 3 casas decimais corretas, iniciando com 𝑥 0 = 0.3 .
Usando o método de Newton determine t (real), com erro relativo inferior a 10 − 2 , tal que a matriz:Seja singular.
Sejam C = (1, 0) e D = (0, 1). Usando o método de Newton para sistemas não lineares determine o valor de um ponto P = (x, y), com precisão de 10−3, que diste 2 unidades de C e de D, obtendo os valores