Enunciado
Cálculo Numérico - Ruggiero - Aspectos Teóricos e Computacionais- Ed: 2º - Capítulo 7.Exercícios - Ex. 7
Use a regra ⅓ de Simpson para integrar a função abaixo entre 0 e 2 com o menor esforço computacional possível(menor número de divisões e maior precisão). Justifique. Trabalhe com três casas decimais.
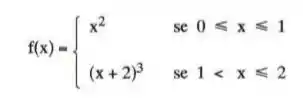
Passo 1
Precisamos dividir essa função em 4 intervalos. Dois intervalos para aproximarmos o polinômio e dois para aproximarmos
Passo 2
Montando a tabela:
Resposta
Exercícios de Livros Relacionados
Determinar h de modo que a regra 3 8 de Simpson forneça o valor de Com erro inferior a 0.5 × 10 − 3 .
Achar o número mínimo de intervalos que se pode usar para, utilizando a regra 1 3 de Simpson obter:Com 4 casas decimais corretas.
Considere a integral:Mostre que o resultado obtido pela regra 1 3 de Simpson com h = 0.5 é surpreendente próximo do resultado exato. Explique por que isso acontece. (sugestão: analise o erro).
Nas integrais do exercício anterior com quantas divisões do intervalo, podemos esperar obter erros menores que 10 − 5 ?
Calcule as integrais a seguir pela regra do trapézio e pelas regras 1 3 𝑒 3 8 de Simpson usando 6 divisões do intervalo de integração. Compare os resultados.