Teoria
Introdução
Fala galera! No último tópico estudamos o Método da Eliminação de Gauss e, de certo modo, vamos continuar estudando ele nesse tópico.
Lembra de quando a gente estava aplicando lá o algoritmo e aparecia um no lugar onde devia ter o pivô? Isso é um belo de um problema porque a gente ia acabar fazendo uma divisão por zero! Bom, quando isso acontecia bastava a gente trocar as linhas pra evitar o problema né? Mas e se isso acontecer com seu computador? Ele tem um algoritmo pré-definido a seguir, que vamos aprender agorinha mesmo.
Outro problema é quando temos um número muito próximo de zero, o que acarreta uma maior propagação de erros. Por exemplo:
A solução desse sistema é dada por . Vamos ver o que acontece quando o resolvemos normalmente utilizando aritmética de ponto flutuante de dígitos. O multiplicador será dado por:
Arredondando para o sistema de dígitos ficamos com . Assim, fazendo os cálculos, temos:
Resolvendo o sistema:
Que é de fato um valor bem próximo de . No entanto, ao substituirmos na primeira equação,
O que deu bem distante do nosso valor correto ! Isso porque o valor muito pequeno no denominador multiplicou aquele errinho de e fez ele ficar muito grande.
Então precisamos de uma forma de contornar esse problema no nosso algoritmo, e é aí que entram as estratégias de pivoteamento.
Pivoteamento Parcial
O que fazemos aqui é o seguinte: a cada etapa em que vamos definir o pivô nós olhamos todos os números abaixo dele e escolhemos como pivô o que tiver maior módulo, fazendo a troca das linhas! Isso faz com que os multiplicadores estejam entre e evitando que os erros por arredondamento aumentem absurdamente. Vamos ver um exemplo:
O primeiro pivô seria o . Mas como estamos aplicando o pivoteamento parcial precisamos comparar os elementos abaixo dele. E como podemos ver, o de maior módulo é o . Logo, fazemos a troca das linhas:
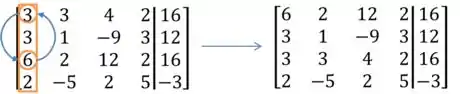
Prosseguindo com a Eliminação de Gauss, chegaríamos ao momento de escolher o próximo pivô:
Dessa vez pra piorar ainda temos o pivô igual à zero! Escolhendo o de maior módulo abaixo dele ficamos com:

Deu pra pegar o espírito né? Lembrando que levamos em conta o módulo como podemos ver no exemplo acima.
Algoritmo do Pivoteamento Parcial
O Pivoteamento Parcial faz uma pequena alteração na Fase 1 do Método de Gauss, na parte da eliminação. A retrosubstituição não é alterada então não iremos repetir seu algoritmo aqui. Segue o algoritmo da fase da eliminação com pivoteamento parcial:
Passo 1. Dados iniciais (o que seu programa vai receber de você):
a. Matriz quadrada (em geral uma matriz é representada como uma lista de listas em programação).
b. Vetor solução (normalmente representado por uma lista).
Passo 2. Percorremos as linhas de com uma variável (de a ).
Passo 3.
Passo 4.
Passo 5.
Passo 6. Se , então e .
Passo 7.
Passo 8. Enquanto , volte para o Passo 6. Caso contrário, continue.
Passo 9. Troque as linhas e de e .
Passo 10. Escolher pivô da -ésima linha e armazenar na variável .
Passo 11. Para cada ‘’, percorremos as linhas de até com uma variável .
Passo 12. Definimos o multiplicador .
Passo 13. Para cada ,
Passo 14. Para cada ‘’, percorremos as colunas de até com uma variável .
Passo 15.
O Algoritmo é exatamente o mesmo, sendo acrescentados apenas os passos a para fazer o pivoteamento quando necessário.
Pivoteamento Completo
O propósito do Pivoteamento Completo é exatamente o mesmo do parcial. A diferença aqui é que além de trocar as linhas ele também pode trocar as colunas! Na comparação de módulo ele leva em conta todos os valores das colunas e linhas seguintes ao pivô. Vamos ver no exemplo que fica mais claro:
Fazendo o Pivoteamento Completo, temos:
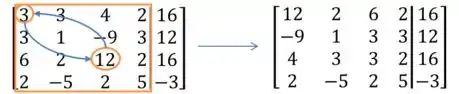
Conseguiu perceber o que aconteceu? Nós trocamos as linhas dos números circulados de lugar e depois trocamos as colunas de lugar também! O cuidado que temos que ter é que ao fazer isso também estamos trocando a ordem das nossas variáveis!!!! E isso é extremamente importante, não se esqueça disso! Tipo pensa em forma de equação:
Trocando as linhas:
Agora trocando as colunas:
Ficou claro? Como trocamos as colunas e de lugar, as variáveis e também trocaram de lugar na nossa matriz! Nesse tipo de questão eu normalmente escrevo em cima das colunas qual variável que ela representa pra eu não me perder, então já fica a dica ;)
Continuando a Eliminação de Gauss com a matriz pivoteada chegamos em:
Aplicando o pivoteamento completo novamente:

Trocamos as colunas novamente! Volto a repetir, tomem cuidado com essa mudança na ordem das variáveis, galera. Deu pra pegar o espírito da coisa né? Vamos ver o algoritmo pra fechar.
Algoritmo do Pivoteamento Completo
Mesmo esquema do pivoteamento parcial. Basta adicionar alguns passos no algoritmo da Fase 1 da Eliminação de Gauss.
Passo 1. Dados iniciais (o que seu programa vai receber de você):
a. Matriz quadrada (em geral uma matriz é representada como uma lista de listas em programação).
b. Vetor solução (normalmente representado por uma lista).
Passo 2. Percorremos as linhas de com uma variável (de a ).
Passo 3.
Passo 4.
Passo 5.
Passo 6.
Passo 7.
Passo 8. Se , então , e .
Passo 9.
Passo 10. Enquanto , volte para o Passo 8. Caso contrário, continue.
Passo 11. e
Passo 12. Enquanto , volte para o Passo 8. Caso contrário, continue.
Passo 13. Troque as linhas e de e .
Passo 14. Troque as colunas e de . Não se esqueça de armazenar essas alterações de alguma forma.
Passo 15. Escolher pivô da -ésima linha e armazenar na variável .
Passo 16. Para cada ‘’, percorremos as linhas de até com uma variável .
Passo 17. Definimos o multiplicador .
Passo 18. Para cada ,
Passo 19. Para cada ‘’, percorremos as colunas de até com uma variável .
Passo 20.
A única coisa que você precisa se lembrar como eu pontuei no Passo 14 é de armazenar em algum lugar essas mudanças de colunas para consertar o resultado da Fase 2, a retrosubstituição.
Obs.: Deu pra perceber que pivoteamento dá um trabalho absurdo né? Não só para você, mas para a máquina também! O pivoteamento parcial é bem justificável já que elimina o problema com os zeros. O pivoteamento completo, no entanto, só é recomendado para sistemas em que a precisão é muito essencial de modo a justificar o tempo extra gasto.
Pivoteamento Parcial
Algoritmo do Pivoteamento Parcial
Pivoteamento Completo
Algoritmo do Pivoteamento Completo
Exercícios Resolvidos
Exercício Resolvido #1
UFRGS-REAMAT-Cálculo Numérico-Livro Scilab.
Resolva o seguinte sistema de equações lineares
Usando eliminação gaussiana com pivotamento parcial (não use o computador para resolver essa questão).
Passo 1
Com esse sistema linear, conseguimos construir essas matrizes:
Começamos passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
Aplicando o pivoteamento parcial:
Como o maior elemento da primeira coluna é o , não precisamos mudar nossa matriz pelo pivoteamento. Mas podemos trocar a segunda e a terceira linhas:
Agora, vamos zerar o primeiro elemento da terceira linha só:
:
Novamente, não será necessário aplicar o pivoteamento parcial, pois o maior elemento da segunda coluna já é o próximo pivô:
:
Passo 3
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
De :
Substituindo em :
Substituindo e em :
Logo, ficamos com:
Resposta
Exercício Resolvido #2
Elaboração Própria.
Utilizando o método da Eliminação de Gauss com pivoteamento parcial, verifique se é possível resolver o sistema linear abaixo:
Passo 1
Com esse sistema linear, conseguimos construir essas matrizes:
Começamos passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
Aplicando o pivoteamento parcial:
Agora, vamos zerar os elementos abaixo do pivô:
:
:
Opa, a última linha zerou por completo... É um caso em que teremos infinitas soluções, já que nosso sistema agora tem 2 equações e 3 incógnitas:
Então, não foi possível resolver o sistema!
Resposta
Sistema possui infinitas soluções
Exercício Resolvido #3
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 380, exercício 4c e 4d.
Resolva os sistemas abaixo utilizando o método da Eliminação de Gauss com pivoteamento parcial:
Passo 1
Começamos passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
Aplicando o pivoteamento parcial:
:
:
:
Aplicando o pivoteamento parcial:
:
:
Passo 3
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
De :
De :
De :
Logo, ficamos com:
Passo 4
Passando para a forma de matriz aumentada:
Passo 5
Fase 1 – Eliminação:
Aplicando o pivoteamento parcial:
:
:
Já ta pivoteado! Continuamos com a eliminação.
:
Passo 6
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
De :
De :
De :
Logo, ficamos com:
Resposta
Exercício Resolvido #4
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 381, exercício 27a.
Resolva o sistema abaixo utilizando o método da Eliminação de Gauss com pivoteamento completo e aritmética de ponto flutuante com dígitos na mantissa e truncamento:
Solução exata:
Passo 1
Começamos passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
Aplicando o pivoteamento:
:
Tomem cuidado porque trocamos as colunas de lugar, então a ordem das soluções foi alterada!
:
Passo 3
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
Da segunda equação:
Substituindo na primeira:
Então temos:
Tivemos um ótimo resultado né? Achamos a solução exata!
Resposta
Exercício Resolvido #5
Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 381, exercício 27b.
Resolva o sistema abaixo utilizando o método da Eliminação de Gauss com pivoteamento completo e aritmética de ponto flutuante com dígitos na mantissa e truncamento:
Solução exata:
Passo 1
Começamos passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
Aplicando o pivoteamento completo:
:
:
:
:
Já está pivoteado então menos trabalho pra gente!
:
Passo 3
Fase 2 – Retrosubstituição:
Passando para a forma de sistema. Lembrando que trocamos as colunas lá no começo!
De :
De :
De :
Logo, ficamos com:
O ficou bastante distante do zero, mas levando em conta que estamos apenas com dígitos na mantissa provavelmente não foi tão ruim haha. O deu certinho. O maior problema foi no mesmo que deu aproximadamente vezes menor que o que deveria.
Resposta
Exercício Resolvido #6
Lista 4 – Professora Suzana – Questão 4
Seja o seguinte sistema linear:
É possível resolvê-lo usando o método de Gauss? Justifique sua resposta. No caso afirmativo aplique o algoritmo, caso contrário use o método de Gauss com pivoteamento parcial.
Passo 1
Claramente não podemos usar o método de Gauss né? Se usássemos teríamos o como primeiro pivô. E o primeiro multiplicador ficaria:
O que é indeterminado né! Vamos aplicar então o método de Gauss com pivoteamento parcial. Passando para a forma matricial:
Passo 2
Fase 1 – Eliminação:
Aplicando o pivoteamento parcial:
:
:
Já está pivoteado ;)
:
Passo 3
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
De :
De :
De :
Logo, ficamos com:
Resposta
Exercício Resolvido #7
Lista 4 – Professora Suzana – Questão 4
Trabalhando com quatro dígitos significativos, resolva os sistemas lineares a seguir (ou detecte que não há solução). Use pivoteamento parcial. Estabeleça um critério para decidir se números pequenos em lugares importantes são considerados como zero ou não. Confira a solução obtida:
Passo 1
Passando para a forma de matriz aumentada:
Passo 2
Fase 1 – Eliminação:
Aplicando o pivoteamento parcial:
:
:
Passo 3
Fase 2 – Retrosubstituição:
Passando para a forma de sistema:
Da segunda equação:
Substituindo na primeira:
Bom, a questão falou pra decidir se números pequenos em lugares importantes iam ser considerados como zero ou não. E esse ta parecendo bem zerado pra mim haha. Então vamos fazer:
Logo, ficamos com:
Beleza, próxima letra.
Passo 4
Passando para a forma de matriz aumentada:
Passo 5
Fase 1 – Eliminação:
Aplicando o pivoteamento parcial:
:
:
Chegamos numa equação que diz
Ou seja, o sistema não tem solução.
Resposta
Sem solução.