Isolamento de Raízes e Método Gráfico
Produzido por Bruno PestanaTeoria
Lá no 8° ano a Tia Marieta nos ensinou como achar as raízes ou os zeros de funções como ou , que são funções do 1° e do 2° grau e a gente fez isso exaustivamente até a fórmula de bháskara ficar grudada no cérebro. Lembrou?
Tá, agora imagina aí se lá, no meio da aula a Tia Marieta falasse:
Ei, turma! Valendo dois pontos na média:
Calcule para mim uma raiz da função ?

É! Se fosse depender disso, naquela época eu não ganharia nem 2 décimos.
Agora vamos aprender como resolver alguns problemas como esse pra nunca mais deixar passar esses 2 pontos. :D
Isolamento de Raízes
Esse estudo que vamos apresentar é válido para funções contínuas, aquelas que quando você desenha o gráfico não tira o lápis do papel, beleza?
Uma coisa que eu sei, é que a raiz de uma função é o valor de para que a minha função seja nula, certo? Logo:
Ta! Eu não sei exatamente as raízes, mas um boa saída é tentar estimar valores para pra ver se eles se aproximam de zero, certo?
Vamos, lá! Fazendo e teremos:
Opa, deu pra perceber o que aconteceu aqui? Quando calculamos tivemos um número positivo e um número negativo. Ou seja, a medida que os valores de x aumentam os valores de que eram positivos passaram a ser negativos.
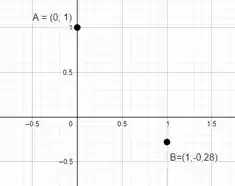
Como se trata de uma função contínua, isso significa que em algum momento a minha função teve que passar pelo zero pois, para os valores de mudarem o sinal então tem que passar pelo eixo x. Então podemos dizer que a nossa função possui uma raiz no intervalo .
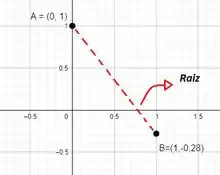
Então, mesmo sem saber o gráfico da função, podemos dizer que a nossa função possui uma raiz no intervalo .
O verdadeiro gráfico da função da função é:
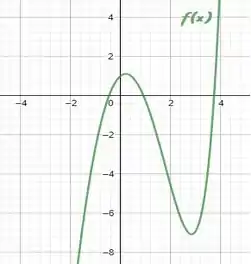
Nossa estimativa estava certa! A função possui uma raiz no intervalo de [0,1].
Se eu tiver um número menor que zero ( nesse caso ) e multiplicar por um número maior que zero (), vamos encontrar um número menor que zero, certo?
Afinal
Traduzindo pro matematiquês, teremos:
Isso a gente pode generalizar para todo e qualquer intervalo, e é isso que o Teorema de Bolzano nos fala:
Se acontecer o caso de , dizemos que existe pelo menos uma raiz com valor igual a () entre o intervalo [a,b].
Esse trabalho de localizar um intervalo o qual contém raízes é o que chamamos de isolar uma raíz.
Aí você me pergunta: Mas, como que eu sei se tem uma ou mais de uma raíz?
Vamos observar apenas o intervalo entre [-1,1] do gráfico .
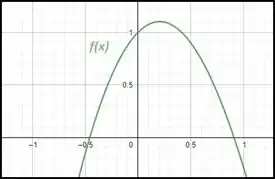
Repara no gráfico no intervalo entre e , nesse intervalo temos duas raízes, certo?
Olhando a forma do gráfico, ele vai “subindo”, chega num ponto máximo e logo depois volta a “descer”.
Isso do gráfico subir e descer tem a ver com o sinal da derivada do gráfico, certo? Se a derivada é positiva, o gráfico está “subindo”, se a derivada é negativa, o gráfico está “descendo”.
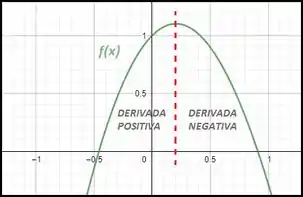
Assim, para que possamos afirmar que num intervalo só tem uma raiz, o sinal da derivada deve ser constante durante todo o intervalo, ou sempre positiva, ou sempre negativa.
Percebe lá entre o intervalo 3 e 4, o gráfico está sempre subindo, logo só temos no máximo uma raiz naquele intervalo.
Logo, se em um intervalo tiver uma raiz e o sinal de num intervalo dado for preservado, teremos apenas uma única raiz.
Método Gráfico para Estimar Raízes.
Existe um método para achar a aproximações de raízes a partir dos gráficos de duas funções.
Vamos lá pegar o exemplo que a professora nos desafiou. Lembra lá:
Certo, para calcular as raízes dessa função, basta igualar a função a zero. Logo:
Ou melhor:
Conseguimos uma equação que iguala duas funções conhecidas. O valor da minha raiz é o pra que essa igualdade seja satisfeita, ou seja, é o ponto de encontro entre o gráfico de com o gráfico de . Faz sentido, né?
Nesse caso, teremos:
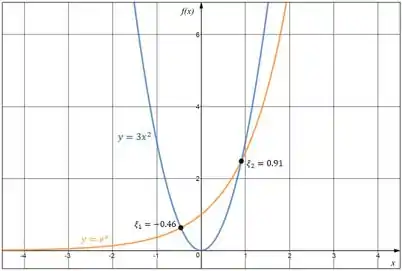
(IMPORTANTE: Você deve separar em duas expressões que você saiba o gráfico para que você consiga desenhar. Nesse exemplo eu poderia muito bem achar a igualdade . Eu mesmo não sei o gráfico de , logo não conseguiria utilizar esse método para achar as raízes.)
Tranquilo?
Como vocês podem ver, onde os gráficos se tocam é o mesmo lugar onde vimos que ficavam as raízes da função original. Saca só:
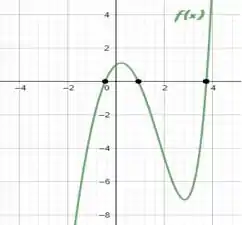
É, ainda tem a terceira raiz, alí próximo do , mas como a professora me pediu apenas uma raiz, já conseguiríamos os dois pontos na média. :P

Só lembrando que aqui nós conseguimos estimar aproximações de raízes, utilizando gráficos e tal. Se quiséssemos fazer isso na mão, teríamos que usar réguas e deixar em escala pra achar o valor mais próximo possível da raiz.
Então tá! Revisando:
Passo 1: Igualar a minha a zero.
Passo 2: passar uma parte da função pro outro lado da igualdade de forma que eu chegue em duas expressões que eu sei o gráfico, algo do tipo
Passo 3: Traça os gráficos e marcar as intersecções.
Passo 4: Olhar no eixo onde os gráficos se tocaram. Aquele ponto é uma raiz da função.
Tudo tranquilo? Vamos exercitar, então?
#PartiuPassar
Método Gráfico para Estimar Raízes.
Exercícios Resolvidos
Exercício Resolvido #1
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 33, exemplo 1.
Determine um intervalo, de amplitude no máximo igual a 1, que contenha uma raiz da função abaixo:
Passo 1
Tá! Vamos lá!
Ele quer o intervalo de no máximo uma unidade cujo esteja localizada uma raiz dessa função. A gente pode notar que é uma equação do 3° grau, logo ela terá três raízes. Mas só precisamos achar o intervalo de apenas uma delas.
Vamos lá?
Passo 2
Primeira coisa a se fazer nesse casos é sair jogando alguns valores pra ver o sinal da função. Eu sugiro sempre iniciar colocando 0, 1 e -1. A maioria dos exercícios eles resolvem bem. Tranquilo?
Fazendo , teremos:
Agora fazendo , vai ficar:
Opa, já achamos o intervalo então, pois pelo Teorema de Bolzano, teremos:
Logo, teremos uma raiz no intervalo que possui uma única unidade.
:D
Resposta
Exercício Resolvido #2
Elaboração Própria
Determine dois intervalos, de amplitude no máximo igual a 1, que contenha duas raízes da função abaixo:
Passo 1
Opa!
Nós temos a funçãozinha e ele quer dois intervalos de uma unidade que isole as duas raízes.
Passo 2
Começando. Vamos chutar os valores de praxe
Opa, mamãe! Já achamos o primeiro intervalo.
Não viu o porquê?
Temos que
Logo e pelo Teorema de Bolzano isso nos garante que existe uma raiz aí nesse intervalo, logo o primeiro intervalo é .
Passo 3
Utilizando , teremos:
É, o não dos deu nada, pois o intervalo de uma unidade mais próxima dele que já conhecemos é , que também é positivo. Logo, pelo Teorema de Bolzano , o que não nos garante uma raiz por ali.
Vamos testar mais alguns valores?
Começando pelo 2.
Também não no diz nada, pois o valor mais próximo conhecido é .
Logo, não tem raiz ali!
Passo 4
Continuando a chutar valores, teremos:
É! Também não nos diz nada, pois também é negativo, logo:
Testando agora (torce aí pra dar certo logo) , vamos ter:

Agora foi, ein? , logo teremos uma raiz nesse intervalo.
Logo, a resposta vai ser:
Resposta
Exercício Resolvido #3
Rubens Vilhena Fonseca, Cálculo Numérico, Belém- Pará, UEPA, 2011, página 16, exercício 03
Dada a função , separe-a em duas funções e aproxime pelo menos uma de suas raízes pelo método gráfico.
Passo 1
É! Temos agora uma questão do método gráfico para estimar raízes! Ele nos deu a função . Vamos que vamos buscar a resposta.
Passo 2
O primeiro passo é igualar a função a zero, já que ele quer a raiz, minha .
Passo 3
Opa! Eu sei o gráfico de , certo? É mais ou menos isso aqui:
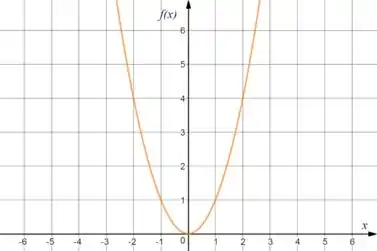
E eu também sei a do . Que é isso aqui:
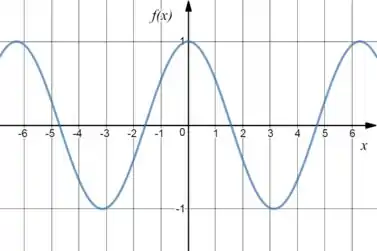
Juntando os dois gráficos, teremos:
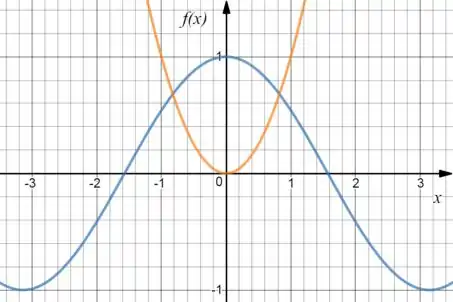
Como ele nos pede apenas uma raiz, escolhendo a raiz positiva, vamos estimar.
Ele está ali pertinho do logo podemos estimar que a raiz é aproximadamente
Resposta
Exercício Resolvido #4
Elaboração Própria
Determine um intervalo, de amplitude no máximo igual a , que contenha três raízes da função abaixo:
Passo 1
Vamos lá?
Temos a função e ele nos pede três raízes num intervalo de duas unidades.
Ideia de como fazer?
Passo 2
É. Eu tenho a sugestão de sempre. Vamos tentar achar os valores da função para
Bora lá?
Até agora temos isso aqui:
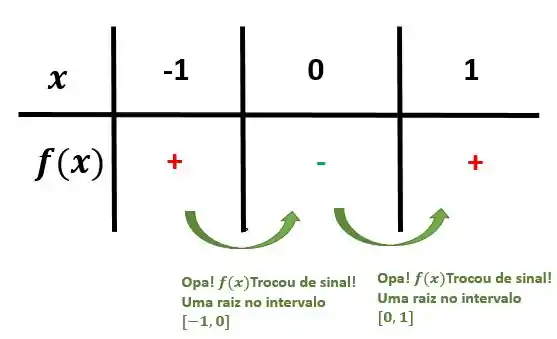
Passo 3
Show! Temos um intervalo de duas unidades, mas só temos duas raízes aí. Vamos tentar ampliar para os valores mais próximos, tipo pra ver no que rola.
E a tabela de valores ficará mais ou menos assim:
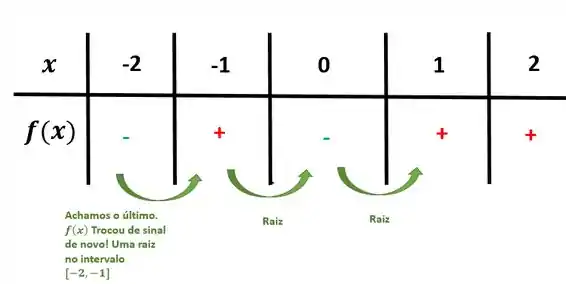
Boa! Isolamos as três raízes. Então acabou o problema, certo?
Errado!
Ele quer um intervalo de no máximo duas unidades. E até agora teríamos o intervalo que possui 3 unidades.

Passo 4
Já sabendo mais ou menos onde estão as raízes, basta agora chutar um intervalo de até duas unidades, pra ver se ele continua obedecendo os critérios da Lei de Bolzano.
Pra fazer isso, tenho que achar um número maior que e menor que que ainda tenha negativo e também temos que achar um número menor que 1 e maior que 0 que já tenha valor de positivo.
Que números você chutaria?
É, eu também!


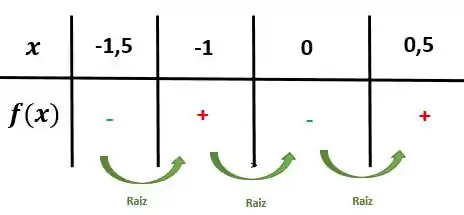
Resolvida a nossa questão. O intervalo é
Resposta
Exercício Resolvido #5
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 95, exercício 1a e 1b.
Localize graficamente as raízes das equações a seguir:
Passo 1
Vamos começar pela letra .
Ele quer pelo método gráfico, logo, teremos que seguir o passo a passo de sempre.
1ª coisa a se fazer é igualar .
Beleza! Eu sei o gráfico do :
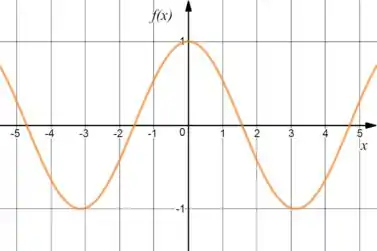
E o do :
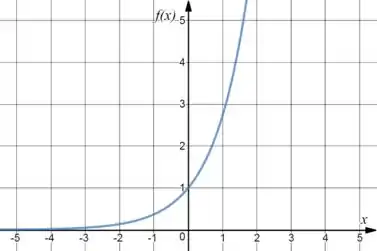
Passo 2
Tá, mas o que eu tenho é e
Em relação ao ele é a mesma função que nós já sabemos, o cosseno, porém com amplitude 4 vezes maior, que vai dar nisso aqui:
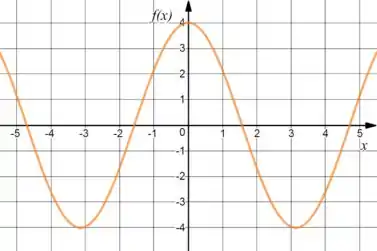
Já no caso do o vai aumentar bem mais rápido, logo o gráfico vai dar uma “achatada” pra junto ao eixo. Logo, teremos:
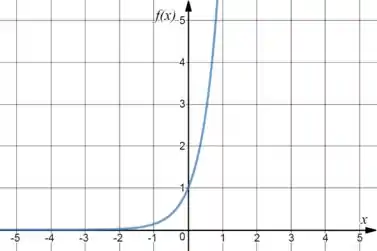
Fazendo a igualdade entre os dois gráficos, vai ficar:
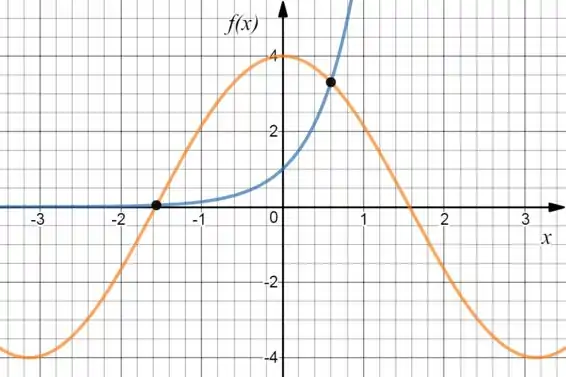
Olhando onde eles se encontram, dá pra estimar mais ou menos as raízes com .
Passo 3
Letra
Fazendo a mesma coisa da letra , teremos:
Encontramos e .
Uma das raízes está na nossa cara. Pra teremos também, logo .
A outra raiz vamos ter que juntar os gráficos:
:
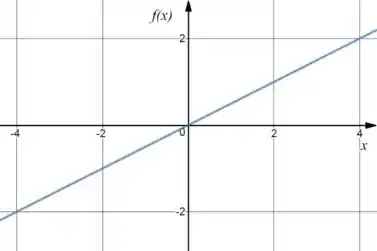
:
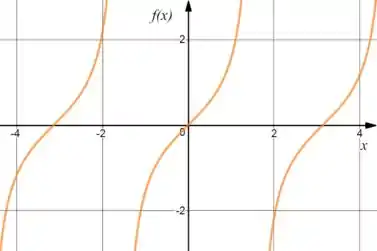
Juntando os dois, teremos:
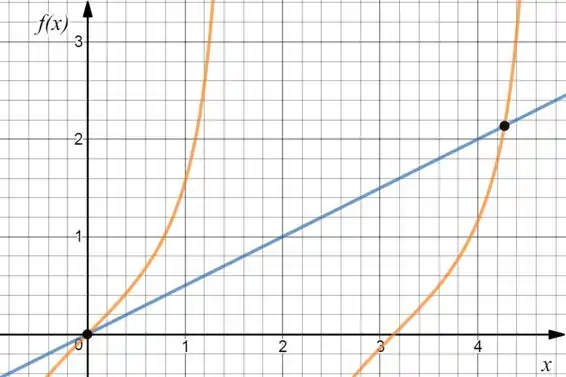
Como podemos ver, uma raiz é o e a outra está mais ou menos localizada no .
Resposta
Exercício Resolvido #6
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 95, exercício 1c.
Localize graficamente as raízes da equação a seguir:
Passo 1
Mais uma pra localizar as raízes pelo método gráfico. Vamos buscá-las!
Temos a função
Primeiro passo de sempre:
Passo 2
Temo que:
Tá, vamos desenhar o gráfico disso?
O gráfico da é de boa, é uma reta horizontal. Mas e o gráfico de , qual é? Eu pelo menos não sei. Então temos que buscar uma saída, uma forma de achar funções que a gente saiba escrever:
Tem alguma ideia?
Eu tenho:
Passa o dividindo pro outro lado, vai ficar:
Agora sim!
Passo 3
Qual o gráfico de ?
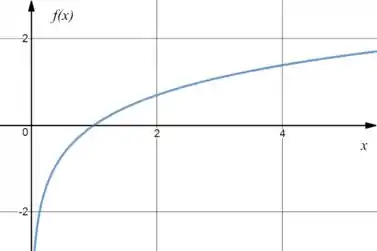
E o gráfico de ?
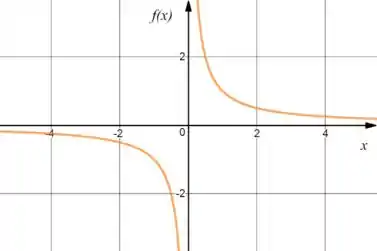
Passo 4
Agora, juntando os gráficos, vamos ter:
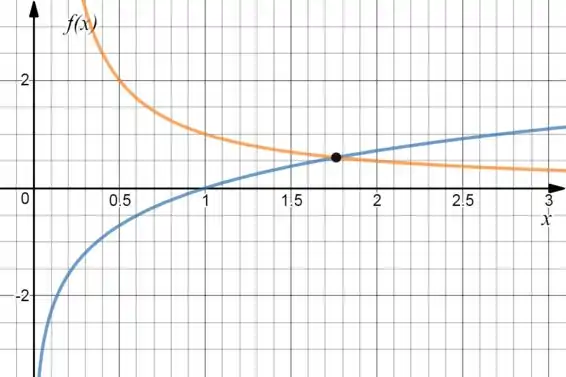
É! Acho que o valor da raiz está ali entre , né?
Como o que nós queremos uma aproximação, acho que uma boa aproximação pra raiz é .
Resposta
Exercício Resolvido #7
Márcia A. Gomes Ruggiero e Vera Lúcia da Rocha Lopes, Cálculo Numérico – Aspectos Teóricos e Computacionais, 2ª ed. São Paulo: MAKRON Books, 1996, pag 95, exercício 1d e 1e.
Localize graficamente as raízes da função a seguir:
Passo 1
Opa, temos duas funçõezinhas aí. Já sabemos o passo a passo, né? Então vamos lá sem mimimi!
:D
Passo 2
Igualar
Tá, temos a nossa
Passo 3
Desenhando o gráfico de cada função, teremos:
:
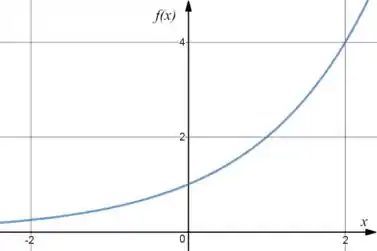
E :
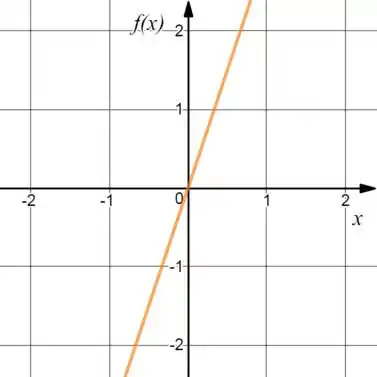
Passo 4
Igualando os dois gráficos, e catando a nossa raiz, vai ficar:
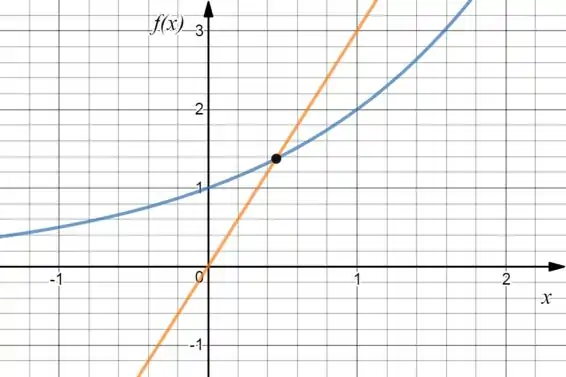
É! Pelo gráfico ele está entre e , né?
Como a ideia é fazer uma aproximação, podemos dizer que:
Passo 5
Igualando , teremos:
Tá! Agora temos que separar em duas funções em que eu saiba desenhar os gráficos das duas, certo?
Temos algo do 3° grau e algo do 1° grau, então vamos separa-los.
Passo 6
Lembra do gráfico do ?
É mais ou menos esse aqui:
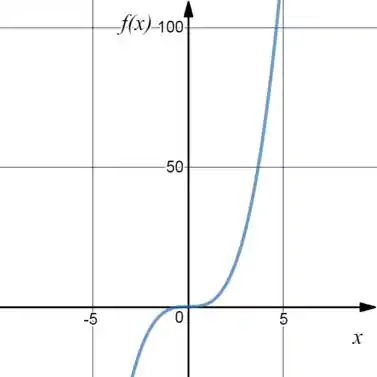
E o é uma reta decrescente, porém “arrastada” em 100 unidades pra cima:
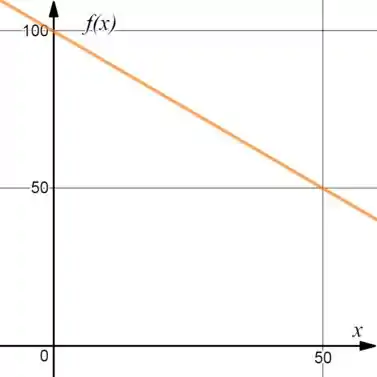
Passo 7
Fazendo a intersecção, ia ficar:
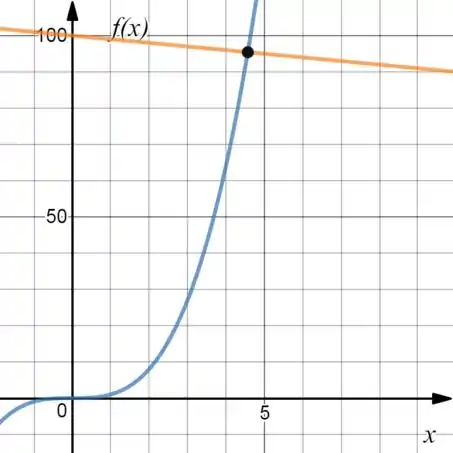
É! Essa raiz está bem no meio do e do . Como queremos a aproximação, vamos dizer que é .
Só toma cuidado que fazer esse exercício no papel pode gerar bastante imprecisão devido à distância adotada. Cuidado quando for fazer! Usando papel milimetrado e usa boa escala pode te ajudar!
#FicaADica
Resposta
Exercício Resolvido #8
Elaboração Própria
Estima Aí a(as) raiz(es) da função abaixo:
Passo 1
Temos uma função nem tão comum de se ver por aí, o Seno Hiperbólico.
Precisamos saber o que é o seno hiperbólico, antes de desenhar, certo?
O seno hiperbólico nada mais nada menos é que:
Então, traduzindo a função, teremos:
Passo 2
Agora sim, temos algo mais palpável.
Seguindo o passo a passo que aprendemos na teoria, teremos:
Igualando .
Passo 3
Agora é só saber os paranauês dos gráficos.
:
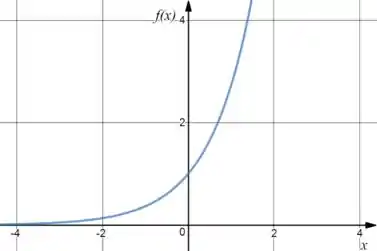
:
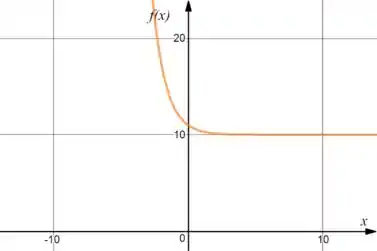
Passo 4
Agora é só igualar os gráficos e ver mais ou menos quais serão as raízes.
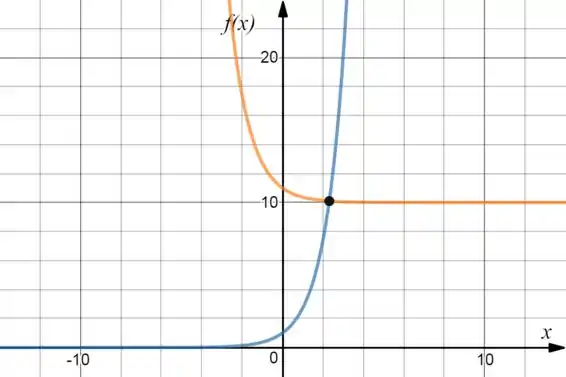
Olhando aí bem mais ou menos, as raízes está entre o e o , um pouco mais próximo do , né? Estimaremos então
Resposta
Exercício Resolvido #9
José Carlos Morais de Araújo Cálculo Numérico, 1ª ed. Rio de Janeiro: Universidade Castelo Branco, 2009, pag 26, exercício 4.
Dada a função , analise esta função e sua derivada pelo gráfico abaixo. Fundamentado neste estudo, responda:
a) Pode existir mais de uma raiz real para a equação ? Justifique.
b) Podemos afirmar que no intervalo existe somente uma raiz real, vemos isso bem analisando o gráfico. Qual teoria discutida anteriormente sustenta esta afirmação quando não temos um gráfico para analisar?
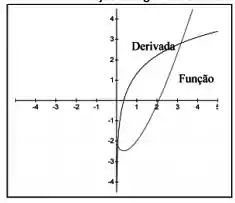
Passo 1
Eita! Questãozinha diferente. Vamos desmembrando-a aos poucos!
1°, na letra a ele nos deu uma função: e ele quer saber se pode existir mais de uma raiz pra essa função aí.
Se liga que sempre quando ele falar em número de raízes você tem que logo associar ao sinal da derivada.
Quando ele pergunta “pode existir mais de uma raiz” pra essa função? Você tem que averiguar, a derivada troca de sinal alguma vez? Se sim, a função pode ter mais de uma raiz.
Nesse caso, no entanto, podemos ver que depois do ponto onde temos o zero da função a derivada é estritamente crescente! Logo, não haverá outra raiz!
Passo 2
Lá na teoria, a gente viu pelo Teorema de Bolzano duas afirmações pra definir e isolar raízes.
- A primeira era que , logo, existem raízes no intervalo .
- Se a função for sempre crescente ou sempre decrescente, só terá no máximo uma raiz.
Nesse caso, a segunda parte do Teorema de Bolzano é a que sustenta a afirmação do texto.

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #10
Elaboração Própria
Ache o valor de para que seja mínimo:
Passo 1
Que isso, cara?
Valor mínimo? Não vimos nada disso até agora!

Relaxaaa Aí!
Vamos só relembrando de quando foi se estudou Cálculo de derivadas. O valor máximo ou mínimo de uma função é dada quando a sua derivada é zero.
Então é isso o que temos que fazer:
Passo 2
Agora deu uma clareada? Temos uma expressão bem mais parecida com os casos mais comuns.
Cortando os 2:
Ou melhor:
Passo 3
Mas pera aí, né? Você não é obrigado a saber a função de . Se rolar de na prova cair alguma questão que você não sabe o gráfico, pega a calculadora (digitando as teclas hyp e sin) e vai jogando alguns valores pra e vai ligando os pontos, até ele ter uma boa cara de gráfico mesmo.
Fazendo isso aqui:
É, um gráfico que cresce super rápido. Fazendo mais alguns valores você vai chegar num negócio assim:
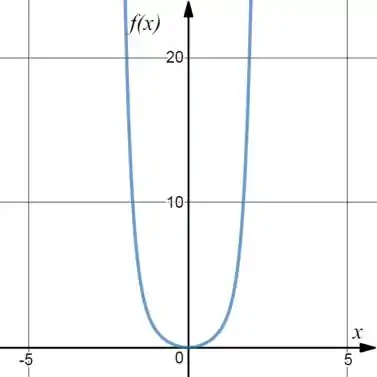
Já pra função , vai ser:
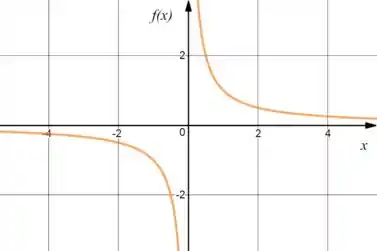
Passo 4
Fazendo a intersecção entre os gráficos, teremos:
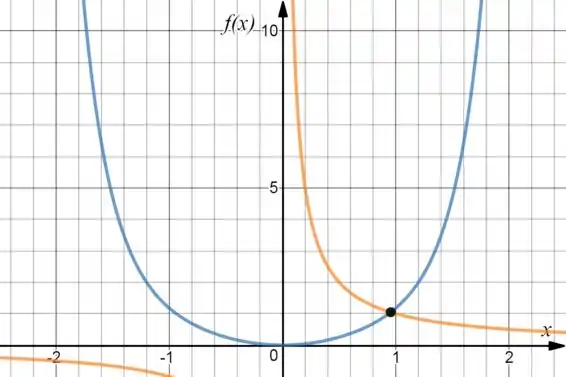
Fazendo uma estimativa pelo gráfico, vamos ter que a raiz dessa função vai ser algo entre e .
Logo: