Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Método da Bissecção

Ver Todos os Exercícios

Teoria

Fala aí! Bora aprender TUDO sobre o Método da Bissecção com o Responde Aí?!

O Método da Bissecção é um tipo de método interativo utilizado pra descobrir os zeros de funções!

Lá no ensino fundamental a gente aprende bhaskara com o objetivo de descobrir os zeros da função em funções de segundo grau, lembra? bhaskara é o que chamamos de método analítico mas em alguns momentos as equações são tão complicadas que é mais fácil usar os métodos interativos!

Imagina que queremos descobrir o zero da função da figura abaixo a partir de métodos analíticos e mais especificamente pelo método da bissecção:

Método da Bissecção
Método da Bissecção

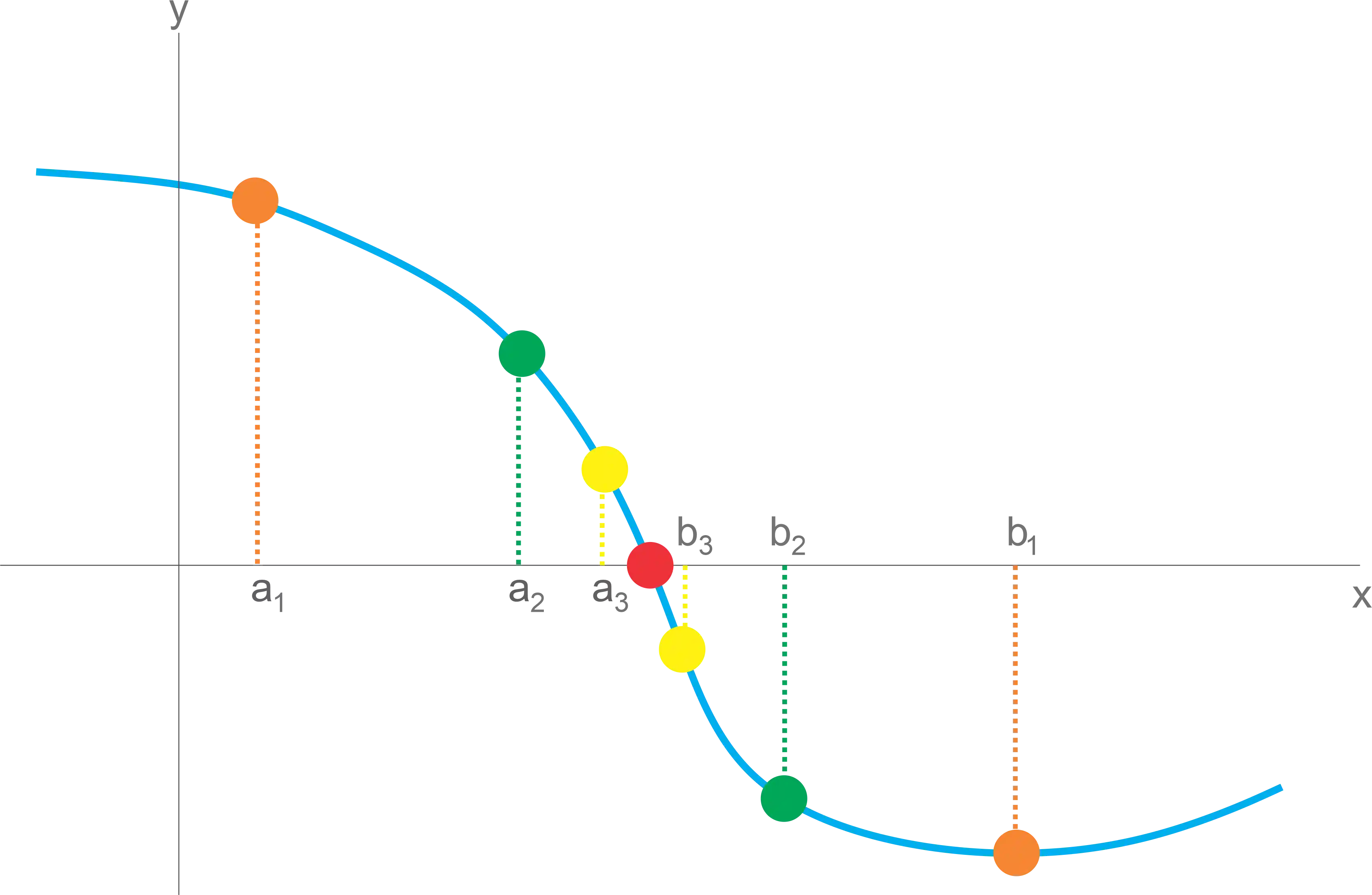
Simplificando muuuito, os métodos interativos são formas inteligentes de chutar uma resposta e depois ir refinando esse chute até chegar em um resultado muito próximo ao resultado analítico, ou seja, o resultado real!

Na figura acima queremos descobrir o zero da função e sabemos que ele fica entre e , usando o método da bissecção, vamos diminuindo esse intervalo até chegar extremamente próximo do resultado!

-Quão próximo?!

Geralmente no enunciado do problema temos um critério de parada, que vai ser a diferença entre o ponto e o ponto . Esse valor vai ser o tamanho do intervalo que a gente foi refinando e ele vai ser bem pequenininho! 😉

Como usar o Método da Bissecção?

A gente vai aprender na prática! Então bora pro exemplo?! Vamos achar o zero da função desse carinha aqui:

Na sua prova, ou lista de exercício o enunciado seria mais ou menos assim:

Em um intervalo de , utilize como critério de parada , onde .Encontre a raíz .

Só pra a gente visualizar melhor, o gráfico da nossa função é esse aqui:

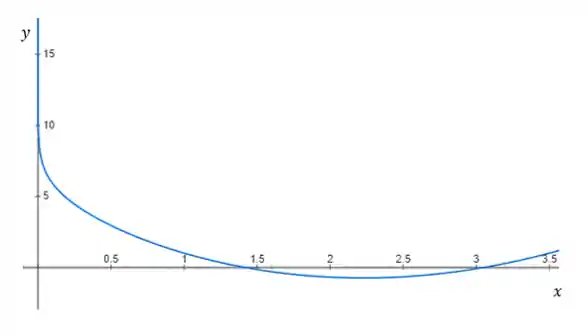
Gráfico da função exemplificada
Gráfico da função exemplificada

Olhando o gráfico a gente sabe que a resposta tá ali perto do , mas sem roubar! vamos seguir o intervalo que o enunciado deu, que é entre e !

Passo 1: Organizando os Dados

A primeira coisa que podemos fazer é montar uma tabelinha show de bola com toooodas as informações que precisamos!

Tabela: Método da Bissecção
Tabela: Método da Bissecção

Nela temos: o número k de iterações é, o valor de   e para cada iteração, os valores de  , e o valor da nossa função  aplicada em : e . E por último e não menos importante: o critério de parada.

Sempre começamos em , já que não foi feita nenhuma iteração antes dessa!

Passo 2: Calculando o f(x) no Intervalo

Podemos calcular o valor da função nos pontos e do intervalo . Se nossa função é:

No ponto :

No ponto :

Passo 3: Calculando

Agora vamos calcular o nosso :

Bom, só falta calcular o valor de no ponto e colocar os valores na tabela. Vamos lá?

Passo 4: Calculando o Critério de Parada

Agora vemos o primeiro critério de parada você lembra qual é ? Isso mesmo, , é só comparar com o erro

Como é maior que o critério de parada, continuamos interagindo. Mas quem eu vou substituir: ou ?

Passo 5: Substituição

Passar saber se vamos reduzir o intervalo substituindo o valor de ou , usamos aquele o seguinte macete:

Macete de substituição
Macete de substituição

No nosso exemplo, temos e :

Então temos:

Como o valor deu negativo, substituímos . Então vamos dar para a nossa máquina o intervalo com erro .

Passo 6: Repetir o Processo até Atingir o Critério de Parada

Agora a gente começa a parte cíclica da coisa! Vamos fazer iterações até chegarmos em um resultado legal! Ah, outra coisa importante é numerar as iterações! Normalmente é pedido isso de vocês.

Vamos jogar os valores na tabela e ver como fica?

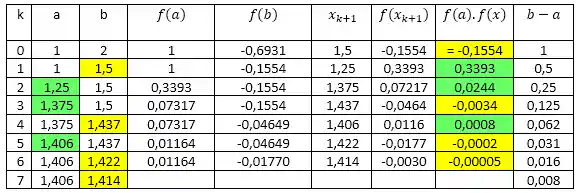
Tabela Resposta: Método da Bissecção
Tabela Resposta: Método da Bissecção

Da uma olhadinha nas cores da tabela, e perceba que a cada valor negativo em
nós substituímos o valor de , caso desse positivo substituímos em . Até chegarmos em um ponto onde :

Opaa, percebeu o que aconteceu aqui?

Nos interagimos até chegar em um intervalo de que é o valor mais próximo que encontramos da nossa raiz aplicada na função!

Percebeu que é bem trabalhoso né? Relaxa que vamos estudar outros métodos mais vantajosos que convergem com muito menos iterações!

Algoritmo

Agora imagina se você quisesse um erro de ? 😱😱😱Aí que ferrou tudo! 🥲

Mas calma, o principal objetivo desse método e de todos os outros que vamos ver é programar as máquinas para fazerem as contas pra gente!

Você provavelmente vai ter que escrever um código no computador. Existem vários programas pra isso, cada um com a sua linguagem, mas de um modo geral elas obedecem o seguinte algoritmo:

  • Passo 1: Dados iniciais (o que seu programa vai receber de você):
    • Intervalo inicial contendo a raiz;
    • Precisão do resultado final
  • Passo 2: Definimos um contador de iterações .
  • Passo 3:
    • Se , então seu intervalo já está ótimo! Escolha um qualquer entre (normalmente se escolhe o ponto médio) e FIM
    • Se não, continue para o Passo 4.
  • Passo 4: , aumentamos uma iteração no contador.
  • Passo 5:
  • Passo 6:
    • Se , fazemos .
    • Se não, fazemos .
  • Passo 7: Voltamos para o Passo 3. Repare que o e o que utilizaremos nesse novo ciclo já não são mais os mesmos e representam um intervalo menor.

No último passo a ordem é voltar pro Passo 3 onde em uma condição a gente para e em outra a gente continua até chegar no Passo 7, quando a gente volta pro Passo 3 e assim por diante, até a condição de parada ser satisfeita e acharmos a nossa resposta! O nome desse processo de repetição é loop!

Ele faz a gente ficar nesse ciclo até que seu programa fique na precisão desejada! Terminado o processo teremos um intervalo contendo a raiz e uma aproximação dela.

Um critério de parada interessante para seu programa e que é normalmente pedido é um número máximo de iterações!

Dessa forma se tiver algum erro no seu programa ou sua função não satisfizer as condições do método você não corre risco de ficar preso em um loop infinito ;)

Se liga nesse vídeo de exercício resolvido sobre método da bissecção que eu separei especialmente pra você:

Agora, vamos praticar com mais exercícios?!

Algoritmo

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Dê um exemplo de função f x , que tenha pelo menos uma raiz que não pode ser determinada pelo método da Bisseção.

Passo 1

Essa eu dei um exemplo na teoria né? A função x 2 não pode ter sua raiz determinada por esse método já que a função não atravessa o eixo x . Qualquer outra função com essa característica também pode ser usada como exemplo, como 7 x 4 = 0 .

Resposta

Qualquer função que toque o eixo x sem atravessá-lo, como por exemplo x 2 = 0 , 7 x 4 = 0 , etc.

Exercício Resolvido #2

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 55, exercício 11a e 11d.

Seja f x = x + 2 x + 1 x x - 1 3 x - 2 . Para qual zero de f o método da bisseção converge quando aplicado nos seguintes intervalos:

a - 3,2.5

b - 1.5,1.75

Passo 1

A primeira coisa é vermos quais são os zeros dessa função que tá bem tranquilo né? Temos x = - 2 ,   - 1 ,   0 ,   1   e 2 como zeros da nossa função. Agora é só aplicar o método da bisseção nesses intervalos até acharmos pra qual desses zeros ele converge:

a   a 0 , b 0 = - 3,2.5

Temos as 5 raízes dentro desse intervalo, então não podemos afirmar para qual delas ele vai convergir.

Iteração 1 :

x 1 = a 0 + b 0 2 = - 0.25

f x 1 = f - 0.25 ≅ - 1.44

f a 0 ∙ f x 1 = - 1920 ∙ - 1.44 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = - 0.25 , 2.5

Ainda temos as raízes 0 , 1 e 2 nesse intervalo então não podemos dizer para qual raiz ele vai convergir.

a 1 , b 1 = - 0.25,2.5

Iteração 2 :

x 2 = a 1 + b 1 2 = 1.125

f x 2 = f 1.125 = - 0.01276

f a 1 ∙ f x 2 = - 1.44 ∙ - 0.01276 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 1.125 , 2.5

Opa, repara que a única raiz nesse intervalo é o 2 ! Então já sabemos que ele vai convergir para o 2 .

Passo 2

b   a 0 , b 0 = - 1.5,1.75

Temos 3 raízes dentro desse intervalo, então não podemos afirmar para qual delas ele vai convergir.

Iteração 1 :

x 1 = a 0 + b 0 2 = 0.125

f x 1 = f 0.125 ≅ 0.375

f a 0 ∙ f x 1 = 20.5078 ∙ 0.375 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 0.125 , 1.75

Opa, repara que a única raiz nesse intervalo é o 1 ! Então já sabemos que ele vai convergir para o 1 .

Resposta

a x = 2

b x = 1

Exercício Resolvido #3

Lista 2 – Professora Aurora – UFPR – Questão 2

A função f x = 2 x - 3 x = 0 possui dois zeros: um no intervalo 0,1 e outro no intervalo 3,4 . Obtenha os zeros dessa função em ambos os intervalos usando o método da bisseção com ε = 10 - 1 . Quantas iterações foram necessárias?

Passo 1

Como todas as questões de bisseção é só aplicar a receita de bolo. Ou para parecer mais engenheiro, basta aplicar o algoritmo!

a 0 , b 0 = 0,1

ε = 0,1

Iteração 1 :

x 1 = a 0 + b 0 2 = 0.5

f x 1 = f 0.5 ≅ - 0.086

f a 0 ∙ f x 1 = 1 ∙ - 0.086 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = 0,0.5

Critério de Parada:

b 1 - a 1 = 0.5 - 0 = 0.5 > 0.1

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 0,0.5

ε = 0,1

Iteração 2 :

x 2 = a 1 + b 1 2 = 0.25

f x 2 = f 0.25 ≅ 0.439

f a 1 ∙ f x 2 = 1 ∙ 0.439 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 0.25,0.5

Critério de Parada:

b 2 - a 2 = 0.5 - 0.25 = 0.25 > 0.1

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 0.25,0.5

ε = 0,1

Iteração 3 :

x 3 = a 2 + b 2 2 = 0.375

f x 3 = f 0.375 ≅ 0.17

f a 2 ∙ f x 3 = 0.439 ∙ 0.17 > 0

Logo, nosso novo intervalo será formado por x 3 e b 2 . Temos então que:

a 3 , b 3 = x 3 , b 2 = 0.375,0.5

Critério de Parada:

b 3 - a 3 = 0.5 - 0.375 = 0.125 > 0.1

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 0.375,0.5

ε = 0,1

Iteração 4 :

x 4 = a 3 + b 3 2 = 0.4375

f x 4 = f 0.4375 ≅ 0.042

f a 3 ∙ f x 4 = 0.17 ∙ 0.042 > 0

Logo, nosso novo intervalo será formado por x 4 e b 3 . Temos então que:

a 4 , b 4 = x 4 , b 3 = 0.4375,0.5

Critério de Parada:

b 3 - a 3 = 0.5 - 0.4375 = 0.0625 < 0.1

Opa! Nosso intervalo está menor que o erro, então podemos parar por aqui e dar como resposta o intervalo 0.4375,0.5 . Uma aproximação para a raiz é o ponto médio do intervalo, x - = 0.46875 .

Passo 2

Beleza, vamos para a próxima raiz:

a 0 , b 0 = 3,4

ε = 0,1

Iteração 1 :

x 1 = a 0 + b 0 2 = 3.5

f x 1 = f 3.5 ≅ 0.814

f a 0 ∙ f x 1 = - 1 ∙ 0.814 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = 3,3.5

Critério de Parada:

b 1 - a 1 = 3.5 - 3 = 0.5 > 0.1

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 3,3.5

ε = 0,1

Iteração 2 :

x 2 = a 1 + b 1 2 = 3.25

f x 2 = f 3.25 ≅ - 0.24

f a 1 ∙ f x 2 = - 1 ∙ - 0.24 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 3.25,3.5

Critério de Parada:

b 2 - a 2 = 3.5 - 3.25 = 0.25 > 0.1

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 3.25,3.5

ε = 0,1

Iteração 3 :

x 3 = a 2 + b 2 2 = 3.375

f x 3 = f 3.375 ≅ 0.25

f a 2 ∙ f x 3 = - 0.24 ∙ 0.25 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = 3.25,3.375

Critério de Parada:

b 3 - a 3 = 3.375 - 3.25 = 0.125 > 0.1

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 3.25,3.375

ε = 0,1

Iteração 4 :

x 4 = a 3 + b 3 2 = 3.3125

f x 4 = f 3.3125 ≅ - 0.0026

f a 3 ∙ f x 4 = - 0.24 ∙ - 0.0026 > 0

Logo, nosso novo intervalo será formado por x 4 e b 3 . Temos então que:

a 4 , b 4 = x 4 , b 3 = 3.3125,3.375

Critério de Parada:

b 3 - a 3 = 3.375 - 3.3125 = 0.0625 < 0.1

Opa! Nosso intervalo está menor que o erro, então podemos parar por aqui e dar como resposta o intervalo 3.3125,3.375 . Uma aproximação possível para a raiz é valor x - = 3.3 4375 .

Resposta

Intervalo 0,1 : x - = 0.46875

Intervalo 3,4 : x - = 3.34375

Foram necessárias 4 iterações para ambos os intervalos.

Exercício Resolvido #4

Lista 2 – Prof Rubens Vilhena Fonseca – UEPA – Capítulo 2.6 – Exercício 7

Calcule a raiz da equação f x = x 2 - 5 s e n x com ε ≤ 0.01 utilizando o método da bisseção. (sugestão utilizar intervalo de busca 1,3 )

Passo 1

Vamos aplicar nosso algoritmo no intervalo que o cara bondosamente sugeriu haha.

a 0 , b 0 = 1,3

ε = 0.01

Iteração 1 :

x 1 = a 0 + b 0 2 = 2

f x 1 = f 2 ≅ - 0.55

f a 0 ∙ f x 1 = - 3.21 ∙ - 3.82 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 2,3

Critério de Parada:

b 1 - a 1 = 3 - 2 = 1 > 0.01

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 2,3

ε = 0.01

Iteração 2 :

x 2 = a 1 + b 1 2 = 2.5

f x 2 = f 2.5 ≅ 3.26

f a 1 ∙ f x 2 = - 0.55 ∙ 3.26 < 0

Logo, nosso novo intervalo será formado por a 1 e x 2 . Temos então que:

a 2 , b 2 = a 1 , x 2 = 2,2.5

Critério de Parada:

b 2 - a 2 = 2.5 - 2 = 0.5 > 0.01

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 2,2.5

ε = 0.01

Iteração 3 :

x 3 = a 2 + b 2 2 = 2.25

f x 3 = f 2.25 ≅ 1.17

f a 2 ∙ f x 3 = - 0.55 ∙ 1.17 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = 2,2.25

Critério de Parada:

b 3 - a 3 = 2.25 - 2 = 0.25 > 0.01

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 2,2.25

ε = 0.01

Iteração 4 :

x 4 = a 3 + b 3 2 = 2.125

f x 4 = f 2.125 ≅ 0.26

f a 3 ∙ f x 4 = - 0.55 ∙ 0.26 < 0

Logo, nosso novo intervalo será formado por a 3 e x 4 . Temos então que:

a 4 , b 4 = a 3 , x 4 = 2,2.125

Critério de Parada:

b 4 - a 4 = 2.125 - 2 = 0.125 > 0.01

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 2,2.125

ε = 0.01

Iteração 5 :

x 5 = a 4 + b 4 2 = 2.0625

f x 5 = f 2.0625 ��� - 0.15

f a 4 ∙ f x 5 = - 0.55 ∙ - 0.15 > 0

Logo, nosso novo intervalo será formado por x 5 e b 4 . Temos então que:

a 5 , b 5 = x 5 , b 4 = 2.0625,2.125

Critério de Parada:

b 5 - a 5 = 2.125 - 2.0625 = 0.0625 > 0.01

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 2.0625,2.125

ε = 0.01

Iteração 6 :

x 6 = a 5 + b 5 2 = 2.09375

f x 6 = f 2.09375 ≅ 0.052

f a 5 ∙ f x 6 = - 0.15 ∙ 0.052 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = 2.0625,2.09375

Critério de Parada:

b 6 - a 6 = 2.09375 - 2.0625 = 0.03125 > 0.01

Como não alcançamos o critério de parada continuamos as iterações.

a 6 , b 6 = 2.0625,2.09375

ε = 0.01

Iteração 7 :

x 7 = a 6 + b 6 2 = 2.078125

f x 7 = f 2.078125 ≅ - 0.052

f a 6 ∙ f x 7 = - 0.15 ∙ - 0.052 > 0

Logo, nosso novo intervalo será formado por x 7 e b 6 . Temos então que:

a 7 , b 7 = x 7 , b 6 = 2.078125,2.09375

Critério de Parada:

b 7 - a 7 = 2.09375 - 2.078125 = 0.015625 > 0.01

Como não alcançamos o critério de parada continuamos as iterações.

a 7 , b 7 = 2.078125,2.09375

ε = 0.01

Iteração 8 :

x 8 = a 7 + b 7 2 = 2.0859375

f x 8 = f 2.0859375 ≅ 0.00002

f a 7 ∙ f x 8 = - 0.052 ∙ 0.00002 < 0

Logo, nosso novo intervalo será formado por a 7 e x 8 . Temos então que:

a 8 , b 8 = a 7 , x 8 = 2.078125,2.0859375

Critério de Parada:

b 8 - a 8 = 2.0859375 - 2.078125 = 0.0078125 < 0.01

Opa! Nosso intervalo (finalmenteeeee) está menor que o erro, então podemos parar por aqui e dar como resposta a aproximação para a raiz x - = 2,0820313 .

Resposta

x - = 2.0820313

Exercício Resolvido #5

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 54, exercícios 5b e 5d

Use o método da Bisseção para encontrar os zeros das funções abaixo com ε ≤ 10 - 3 :

a   f x = e x - x 2 + 3 x - 2 no intervalo 0,1

b   f x = x c o s x - 2 x 2 + 3 x - 1 no intervalo 0.2,0.3

Passo 1

Novamente, é só aplicarmos o algoritmo. Dessa vez os números vão ficar beeeem grandes então como ele pede uma precisão de 10 - 3 vamos usar pelo menos 4 casas decimais pra não ter problema:

a a 0 , b 0 = 0,1

ε = 0.001

Iteração 1 :

x 1 = a 0 + b 0 2 = 0.5

f x 1 = f 0.5 ≅ 0.9

f a 0 ∙ f x 1 = - 1 ∙ 0.9 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = 0,0.5

Critério de Parada:

b 1 - a 1 = 0.5 - 0 = 0.5 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 0,0.5

ε = 0.001

Iteração 2 :

x 2 = a 1 + b 1 2 = 0.25

f x 2 = f 0.25 ≅ - 0.03

f a 1 ∙ f x 2 = - 1 ∙ - 0.03 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 0.25,0.5

Critério de Parada:

b 2 - a 2 = 0.5 - 0.25 = 0.25 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 0.25,0.5

ε = 0.001

Iteração 3 :

x 3 = a 2 + b 2 2 = 0.375

f x 3 = f 0.375 ≅ 0.44

f a 2 ∙ f x 3 = - 0.03 ∙ 0.44 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = 0.25,0.375

Critério de Parada:

b 3 - a 3 = 0.375 - 0.25 = 0.125 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 0.25,0.375

ε = 0.001

Iteração 4 :

x 4 = a 3 + b 3 2 = 0.3125

f x 4 = f 0.3125 ≅ 0.2

f a 3 ∙ f x 4 = - 0.03 ∙ 0.2 < 0

Logo, nosso novo intervalo será formado por a 3 e x 4 . Temos então que:

a 4 , b 4 = a 3 , x 4 = 0.25,0.3125

Critério de Parada:

b 4 - a 4 = 0.3125 - 0.25 = 0.0625 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 0.25,0.3125

ε = 0.001

Iteração 5 :

x 5 = a 4 + b 4 2 = 0.28125

f x 5 = f 0.28125 ≅ 0.09

f a 4 ∙ f x 5 = - 0.3 ∙ 0.09 < 0

Logo, nosso novo intervalo será formado por a 4 e x 5 . Temos então que:

a 5 , b 5 = a 4 , x 5 = 0.25,0.28125

Critério de Parada:

b 5 - a 5 = 0.28125 - 0.25 = 0.03125 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 0.25,0.28125

ε = 0.001

Iteração 6 :

x 6 = a 5 + b 5 2 = 0.265625

f x 6 = f 2.09375 ≅ 0.03

f a 5 ∙ f x 6 = - 0.03 ∙ 0.03 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = 0.25,0.265625

Critério de Parada:

b 6 - a 6 = 0.265625 - 0.25 = 0.015625 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 6 , b 6 = 0.25,0.265625

ε = 0.001

Iteração 7 :

x 7 = a 6 + b 6 2 = 0.2578

f x 7 = f 0.2578 ≅ 0.001

f a 6 ∙ f x 7 = - 0.03 ∙ 0.001 < 0

Logo, nosso novo intervalo será formado por a 6 e x 7 . Temos então que:

a 7 , b 7 = a 6 , x 7 = 0.25,0.2578

Critério de Parada:

b 7 - a 7 = 0.2578 - 0.25 = 0.0078 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 7 , b 7 = 0.25,0.2578

ε = 0.001

Iteração 8 :

x 8 = a 7 + b 7 2 = 0.2539

f x 8 = f 0.2539 ≅ - 0.014

f a 7 ∙ f x 8 = - 0.03 ∙ - 0.014 > 0

Logo, nosso novo intervalo será formado por x 8 e b 7 . Temos então que:

a 8 , b 8 = x 8 , b 7 = 0.2539,0.2578

Critério de Parada:

b 8 - a 8 = 0.2578 - 0.2539 = 0.0039 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 8 , b 8 = 0.2539,0.2578

ε = 0.001

Iteração 9 :

x 9 = a 8 + b 8 2 = 0.2559

f x 9 = f 0.2559 ≅ - 0.006

f a 8 ∙ f x 9 = - 0.014 ∙ - 0.006 > 0

Logo, nosso novo intervalo será formado por x 9 e b 8 . Temos então que:

a 9 , b 9 = x 9 , b 8 = 0.2559,0.2578

Critério de Parada:

b 9 - a 9 = 0.2578 - 0.2559 = 0.0019 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 9 , b 9 = 0.2559,0.2578

ε = 0.001

Iteração 10 :

x 10 = a 9 + b 9 2 = 0.2568

f x 10 = f 0.2568 ≅ - 0.003

f a 9 ∙ f x 10 = - 0.006 ∙ - 0.003 > 0

Logo, nosso novo intervalo será formado por x 10 e b 9 . Temos então que:

a 10 , b 10 = x 10 , b 9 = 0.2568,0.2578

Critério de Parada:

b 10 - a 10 = 0.2578 - 0.2568 = 0.001 = 0.001

Opa! Nosso intervalo está igual ao erro, então podemos parar por aqui e dar como resposta a aproximação para a raiz x - = 0.2573 .

Passo 2

Ufa! Agora vamos para a letra b .

a 0 , b 0 = 0.2,0.3

ε = 0.001

Iteração 1 :

x 1 = a 0 + b 0 2 = 0.25

f x 1 = f 0.25 ≅ - 0.13

f a 0 ∙ f x 1 = - 0.28 ∙ - 0.13 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 0.25,0.3

Critério de Parada:

b 1 - a 1 = 0.3 - 0.25 = 0.05 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 0.25,0.3

ε = 0.001

Iteração 2 :

x 2 = a 1 + b 1 2 = 0.275

f x 2 = f 0.275 ≅ - 0.06

f a 1 ∙ f x 2 = - 0.13 ∙ - 0.06 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 0.275,0.3

Critério de Parada:

b 2 - a 2 = 0.3 - 0.275 = 0.025 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 0.275,0.3

ε = 0.001

Iteração 3 :

x 3 = a 2 + b 2 2 = 0.2875

f x 3 = f 0.2875 ≅ - 0.03

f a 2 ∙ f x 3 = - 0.06 ∙ - 0.03 > 0

Logo, nosso novo intervalo será formado por x 3 e b 2 . Temos então que:

a 3 , b 3 = x 3 , b 2 = 0.2875,0.3

Critério de Parada:

b 3 - a 3 = 0.3 - 0.2875 = 0.0125 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 0.2875,0.3

ε = 0.001

Iteração 4 :

x 4 = a 3 + b 3 2 = 0.29375

f x 4 = f 0.29375 ≅ - 0.01

f a 3 ∙ f x 4 = - 0.03 ∙ - 0.01 > 0

Logo, nosso novo intervalo será formado por a 3 e x 4 . Temos então que:

a 4 , b 4 = x 4 , b 3 = 0.29375,0.3

Critério de Parada:

b 4 - a 4 = 0.3 - 0.29375 = 0.00625 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 0.29375,0.3

ε = 0.001

Iteração 5 :

x 5 = a 4 + b 4 2 = 0.2969

f x 5 = f 0.2969 ≅ - 0.002

f a 4 ∙ f x 5 = - 0.01 ∙ - 0.002 > 0

Logo, nosso novo intervalo será formado por x 5 e b 4 . Temos então que:

a 5 , b 5 = x 5 , b 4 = 0.2969,0.3

Critério de Parada:

b 5 - a 5 = 0.3 - 0.2969 = 0.0031 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 0.2969,0.3

ε = 0.001

Iteração 6 :

x 6 = a 5 + b 5 2 = 0.2984

f x 6 = f 0.2984 ≅ 0.002

f a 5 ∙ f x 6 = - 0.002 ∙ 0.002 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = 0.2969,0.2984

Critério de Parada:

b 6 - a 6 = 0.2984 - 0.2969 = 0.0015 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 6 , b 6 = 0.2969,0.2984

ε = 0.001

Iteração 7 :

x 7 = a 6 + b 6 2 = 0.2977

f x 7 = f 0.2977 ≅ 0.0003

f a 6 ∙ f x 7 = - 0.002 ∙ 0.0003 < 0

Logo, nosso novo intervalo será formado por a 6 e x 7 . Temos então que:

a 7 , b 7 = a 6 , x 7 = 0.2969,0.2977

Critério de Parada:

b 7 - a 7 = 0.2977 - 0.2969 = 0.0008 < 0.001

Opa! Nosso intervalo está menor que o erro, então podemos parar por aqui e dar como resposta a aproximação para a raiz x - = 0.2973 .

Resposta

a   x - = 0.2573

b x - = 0.2973

Exercício Resolvido #6

Richard L. Burden e J. Douglas Faires, Numerical Analysis, 9ª ed. Brooks/Cole, Cengage Learning, pag 55, exercício 13

Encontre uma aproximação para 25 3 com precisão de 10 - 2 usando o método da Bisseção.

Passo 1

Opa, finalmente uma questão pra gente raciocinar um pouco. Bom, o método da Bisseção nos dá o zero de uma função, certo? Po, mas essa questão não ta dando função nenhuma! Alguma ideia?

Bom, pensa comigo, quanto vale 25 3 elevado ao cubo? Vale 25 né? Então:

25 3 3 = 25

25 3 3 - 25 = 0

x 3 - 25 = 0

E pronto! Taí nossa função! O x que zera a função f x = x 3 - 25 é justamente o x = 25 3 que é o que queremos aproximar! O próximo passo é arrumar um intervalo que contenha 25 3 . Que tal 2.5 e 3 ? Se liga:

2,5 3 - 25 = - 9.375

3 3 - 25 = 2

Opa, um deu positivo e o outro negativo, então temos nosso intervalo 2.5,3 . Agora é só aplicar o algoritmo ;)

Passo 2

a 0 , b 0 = 2.5,3

ε = 0.0 1

Iteração 1 :

x 1 = a 0 + b 0 2 = 2.75

f x 1 = f 2.75 ≅ - 4.2

f a 0 ∙ f x 1 = - 9.375 ∙ - 4.2 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 2.75,3

Critério de Parada:

b 1 - a 1 = 3 - 2.75 = 0 . 25 > 0 . 01

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 2.75,3

ε = 0.0 1

Iteração 2 :

x 2 = a 1 + b 1 2 = 2.875

f x 2 = f 2.875 ≅ - 1.2 4

f a 1 ∙ f x 2 = - 4.2 ∙ - 1.2 4 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 2.875 , 3

Critério de Parada:

b 2 - a 2 = 3 - 2.875 = 0.125 > 0.0 1

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 2.875,3

ε = 0 . 01

Iteração 3 :

x 3 = a 2 + b 2 2 = 2.9375

f x 3 = f 2.9375 ≅ 0.35

f a 2 ∙ f x 3 = - 1.24 ∙ 0.35 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = 2.875 , 2.9375

Critério de Parada:

b 3 - a 3 = 2.9375 - 2.875 = 0.0625 > 0 . 01

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 2.875 , 2.9375

ε = 0 . 01

Iteração 4 :

x 4 = a 3 + b 3 2 = 2.90625

f x 4 = f 2.90625 ≅ - 0.45

f a 3 ∙ f x 4 = - 1.24 ∙ - 0.45 > 0

Logo, nosso novo intervalo será formado por x 4 e b 3 . Temos então que:

a 4 , b 4 = x 4 , b 3 = 2.90625 , 2.9375

Critério de Parada:

b 4 - a 4 = 2.9375 - 2.90625 = 0.03125 > 0.0 1

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 2.90625 , 2.9375

ε = 0 . 01

Iteração 5 :

x 5 = a 4 + b 4 2 = 2.92 2

f x 5 = f 2.92 2 ≅ - 0.05

f a 4 ∙ f x 5 = - 0.45 ∙ - 0.05 > 0

Logo, nosso novo intervalo será formado por x 5 e b 4 . Temos então que:

a 5 , b 5 = a 4 , x 5 = 2.92 2 , 2.9375

Critério de Parada:

b 5 - a 5 = 2.9375 - 2.92 2 = 0.0155 > 0 . 01

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 2.92 2 , 2.9375

ε = 0 . 01

Iteração 6 :

x 6 = a 5 + b 5 2 = 2.929 7

f x 6 = f 2.929 7 ≅ 0.14

f a 5 ∙ f x 6 = - 0.05 ∙ 0.14 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = 2.92 2 , 2.929 7

Critério de Parada:

b 6 - a 6 = 2.929 7 - 2.92 2 = 0.0 077 < 0.01

Nosso intervalo está menor que o erro, então podemos parar por aqui e dar como resposta a aproximação para a raiz x - = 2.926 .

Resposta

x - = 2.926

Exercício Resolvido #7

Lista 2 – Professor Daniel – UFRJ – Questão 3

Encontre o número de iterações necessário para obter uma aproximação com precisão de 10 - 3 para a solução da equação x 3 + x - 4 = 0 que se encontra no intervalo 1,2 pelo Método da Bisseção. Encontre um valor aproximado para a raiz com esse grau de precisão.

Passo 1

Primeira coisa que ele pergunta é quantas iterações vamos precisar. Pra isso basta usar nossa fórmula né?

k > ln ⁡ b 0 - a 0 - ln ⁡ ε ln ⁡ 2 = ln ⁡ 1 - ln ⁡ 0.001 ln ⁡ 2 ≅ 9.96 ⇒ k = 10

Beleza, então vamos precisar de 10 iterações! Agora temos que botar a mão na massa e achar uma aproximação pra isso aí.

Passo 2

a 0 , b 0 = 1,2

ε = 0.001

Iteração 1 :

x 1 = a 0 + b 0 2 = 1.5

f x 1 = f 1.5 ≅ 0.875

f a 0 ∙ f x 1 = - 2 ∙ 0.875 < 0

Logo, nosso novo intervalo será formado por a 0 e x 1 . Temos então que:

a 1 , b 1 = a 0 , x 1 = 1,1.5

Critério de Parada:

b 1 - a 1 = 1.5 - 1 = 0.5 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 1,1.5

ε = 0.001

Iteração 2 :

x 2 = a 1 + b 1 2 = 1.25

f x 2 = f 1.25 ≅ - 0.8

f a 1 ∙ f x 2 = - 2 ∙ - 0.8 > 0

Logo, nosso novo intervalo será formado por x 2 e b 1 . Temos então que:

a 2 , b 2 = x 2 , b 1 = 1.25,1.5

Critério de Parada:

b 2 - a 2 = 1.5 - 1.25 = 0.25 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 1.25,1.5

ε = 0.001

Iteração 3 :

x 3 = a 2 + b 2 2 = 1.375

f x 3 = f 1.375 ≅ - 0.03

f a 2 ∙ f x 3 = - 0.8 ∙ - 0.03 > 0

Logo, nosso novo intervalo será formado por x 3 e b 2 . Temos então que:

a 3 , b 3 = x 3 , b 2 = 1.375,1.5

Critério de Parada:

b 3 - a 3 = 1.5 - 1.375 = 0.125 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 1.375,1.5

ε = 0.001

Iteração 4 :

x 4 = a 3 + b 3 2 = 1.4375

f x 4 = f 1.4375 ≅ 0.4

f a 3 ∙ f x 4 = - 0.03 ∙ 0.4 < 0

Logo, nosso novo intervalo será formado por a 3 e x 4 . Temos então que:

a 4 , b 4 = a 3 , x 4 = 1.375,1.4375

Critério de Parada:

b 4 - a 4 = 1.4375 - 1.375 = 0.0625 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 1.375,1.4375

ε = 0.001

Iteração 5 :

x 5 = a 4 + b 4 2 = 1.40625

f x 5 = f 1.40625 ≅ 0.2

f a 4 ∙ f x 5 = - 0.03 ∙ 0.2 < 0

Logo, nosso novo intervalo será formado por a 4 e x 5 . Temos então que:

a 5 , b 5 = a 4 , x 5 = 1.375,1.40625

Critério de Parada:

b 5 - a 5 = 1.40625 - 1.375 = 0.03125 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 1.375,1.40625

ε = 0.001

Iteração 6 :

x 6 = a 5 + b 5 2 = 1.390625

f x 6 = f 1.390625 ≅ 0.08

f a 5 ∙ f x 6 = - 0.03 ∙ 0.08 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = 1.375,1.390625

Critério de Parada:

b 6 - a 6 = 1.390625 - 1.375 = 0.015625 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 6 , b 6 = 1.375,1.390625

ε = 0.001

Iteração 7 :

x 7 = a 6 + b 6 2 = 1.3828

f x 7 = f 1.3828 ≅ 0.03

f a 6 ∙ f x 7 = - 0.03 ∙ 0.03 < 0

Logo, nosso novo intervalo será formado por a 6 e x 7 . Temos então que:

a 7 , b 7 = a 6 , x 7 = 1.375,1.3828

Critério de Parada:

b 7 - a 7 = 1.3828 - 1.375 = 0.0078 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 7 , b 7 = 1.375,1.3828

ε = 0.001

Iteração 8 :

x 8 = a 7 + b 7 2 = 1.3789

f x 8 = f 1.3789 ≅ 0.0007

f a 7 ∙ f x 8 = - 0.03 ∙ 0.0007 < 0

Logo, nosso novo intervalo será formado por a 7 e x 8 . Temos então que:

a 8 , b 8 = a 7 , x 8 = 1.375,1.3789

Critério de Parada:

b 8 - a 8 = 1.3789 - 1.375 = 0.0039 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 8 , b 8 = 1.375,1.3789

ε = 0.001

Iteração 9 :

x 9 = a 8 + b 8 2 = 1.3769

f x 9 = f 1.3769 ≅ - 0.01

f a 8 ∙ f x 9 = - 0.03 ∙ - 0.01 > 0

Logo, nosso novo intervalo será formado por x 9 e b 8 . Temos então que:

a 9 , b 9 = x 9 , b 8 = 1.3769,1.3789

Critério de Parada:

b 9 - a 9 = 1.3789 - 1.3769 = 0.002 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 9 , b 9 = 1.3769,1.3789

ε = 0.001

Iteração 10 :

x 10 = a 9 + b 9 2 = 1.3779

f x 10 = f 1.3779 ≅ - 0.006

f a 9 ∙ f x 10 = - 0.01 ∙ - 0.006 > 0

Logo, nosso novo intervalo será formado por x 10 e b 9 . Temos então que:

a 10 , b 10 = x 10 , b 9 = 1.3779,1.3789

Critério de Parada:

b 10 - a 10 = 1.3789 - 1.3779 = 0.001 = 0.001

Opa! Nosso intervalo está igual ao erro, então podemos parar por aqui e dar como resposta a aproximação para a raiz x - = 1.3784 .

Resposta

São necessárias 10 iterações. x - = 1.3784 .

Exercício Resolvido #8

Lista 2 – Professora Juliana – UFRJ – Questão 2 – Item ii

Seja f x = cos ⁡ x - x em 0,1 , faça:

a Mostre que f x é contínua no intervalo e teste se existe uma raiz no intervalo.

b Encontre o número de iterações k para uma precisão de ε = 10 - 3 usando o método da bisseção.

c Faça k iterações e forneça uma estimativa para a raiz.

Passo 1

a Sabemos que cos ⁡ x e x são contínuas em 0,1 né? Então f x também será! Repare que teríamos problemas apenas se estivéssemos em um intervalo negativo já que começaríamos a mexer com imaginários.

Para testar se tem uma raiz basta usarmos o teorema do nosso amigo com nome de palhaço, o grande Bolzano.

f 0 = 1

f 1 = cos ⁡ 1 - 1 ≅ - 0.46

Temos f 0 ∙ f 1 < 0 , logo existe uma raiz nesse intervalo.

Passo 2

b Agora para acharmos o número de iterações só jogarmos naquela fórmula:

k > ln ⁡ b 0 - a 0 - ln ⁡ ε ln ⁡ 2 = ln ⁡ 1 - ln ⁡ 0.001 ln ⁡ 2 ≅ 9.96 ⇒ k = 10

Beleza, precisamos de 10 iterações! Agora vamos botar a mão na massa!

Passo 3

c a 0 , b 0 = 0,1

ε = 0.001

Iteração 1 :

x 1 = a 0 + b 0 2 = 0.5

f x 1 = f 0.5 ≅ 0.17

f a 0 ∙ f x 1 = 1 ∙ 0.17 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 0.5,1

Critério de Parada:

b 1 - a 1 = 1 - 0.5 = 0.5 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 0.5,1

ε = 0.001

Iteração 2 :

x 2 = a 1 + b 1 2 = 0.75

f x 2 = f 0.75 ≅ - 0.13

f a 1 ∙ f x 2 = 0.17 ∙ - 0.13 < 0

Logo, nosso novo intervalo será formado por a 1 e x 2 . Temos então que:

a 2 , b 2 = a 1 , x 2 = 0.5,0.75

Critério de Parada:

b 2 - a 2 = 0.75 - 0.5 = 0.25 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 0.5,0.75

ε = 0.001

Iteração 3 :

x 3 = a 2 + b 2 2 = 0.625

f x 3 = f 0.625 ≅ 0.02

f a 2 ∙ f x 3 = 0.17 ∙ 0.02 > 0

Logo, nosso novo intervalo será formado por x 3 e b 2 . Temos então que:

a 3 , b 3 = x 3 , b 2 = 0.625 , 0.75

Critério de Parada:

b 3 - a 3 = 0.75 - 0.625 = 0.125 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 0.625 , 0.75

ε = 0.001

Iteração 4 :

x 4 = a 3 + b 3 2 = 0.6875

f x 4 = f 0.6875 ≅ - 0.0 6

f a 3 ∙ f x 4 = 0.02 ∙ - 0.0 6 < 0

Logo, nosso novo intervalo será formado por a 3 e x 4 . Temos então que:

a 4 , b 4 = a 3 , x 4 = 0.625 , 0.6875

Critério de Parada:

b 4 - a 4 = 0.6875 - 0.625 = 0.0625 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 0.625 , 0.6875

ε = 0.001

Iteração 5 :

x 5 = a 4 + b 4 2 = 0.65625

f x 5 = f 0.65625 ≅ - 0.02

f a 4 ∙ f x 5 = 0.02 ∙ - 0.02 < 0

Logo, nosso novo intervalo será formado por a 4 e x 5 . Temos então que:

a 5 , b 5 = a 4 , x 5 = 0.625 , 0.65625

Critério de Parada:

b 5 - a 5 = 0.65625 - 0.625 = 0.03125 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 0.625 , 0.65625

ε = 0.001

Iteração 6 :

x 6 = a 5 + b 5 2 = 0.640625

f x 6 = f 0.640625 ≅ 0.001

f a 5 ∙ f x 6 = 0.02 ∙ 0.001 > 0

Logo, nosso novo intervalo será formado por x 6 e b 5 . Temos então que:

a 6 , b 6 = x 6 , b 5 = 0.640625 , 0.65625

Critério de Parada:

b 6 - a 6 = 0.65625 - 0.640625 = 0.015625 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 6 , b 6 = 0.640625 , 0.65625

ε = 0.001

Iteração 7 :

x 7 = a 6 + b 6 2 = 0.6484

f x 7 = f 0.6484 ≅ - 0.008

f a 6 ∙ f x 7 = 0.001 ∙ - 0.008 < 0

Logo, nosso novo intervalo será formado por a 6 e x 7 . Temos então que:

a 7 , b 7 = a 6 , x 7 = 0.6406 , 0.6484

Critério de Parada:

b 7 - a 7 = 0.6484 - 0.6406 = 0.0078 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 7 , b 7 = 0.6406 , 0.6484

ε = 0.001

Iteração 8 :

x 8 = a 7 + b 7 2 = 0.64453

f x 8 = f 0.64453 ≅ - 0.003

f a 7 ∙ f x 8 = 0.001 ∙ - 0.003 < 0

Logo, nosso novo intervalo será formado por a 7 e x 8 . Temos então que:

a 8 , b 8 = a 7 , x 8 = 0.6406 , 0.64453

Critério de Parada:

b 8 - a 8 = 0.64453 - 0.6406 = 0.0039 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 8 , b 8 = 0.6406 , 0.64453

ε = 0.001

Iteração 9 :

x 9 = a 8 + b 8 2 = 0 . 6426

f x 9 = f 0 . 6426 ≅ - 0.001

f a 8 ∙ f x 9 = 0.001 ∙ - 0.001 < 0

Logo, nosso novo intervalo será formado por a 8 e x 9 . Temos então que:

a 9 , b 9 = a 8 , x 9 = 0.6406 , 0 . 6426

Critério de Parada:

b 9 - a 9 = 0 . 6426 - 0.6406 = 0.002 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 9 , b 9 = 0.6406 , 0 . 6426

ε = 0.001

Iteração 10 :

x 10 = a 9 + b 9 2 = 0.6416

f x 10 = f 0.6416 ≅ 0.0001

f a 9 ∙ f x 10 = 0.001 ∙ 0.0001 > 0

Logo, nosso novo intervalo será formado por x 10 e b 9 . Temos então que:

a 10 , b 10 = x 10 , b 9 = 0.6416 , 0 . 6426

Critério de Parada:

b 10 - a 10 = 0 . 6426 - 0 . 64 1 6 = 0.001 = 0.001

Finalmente! Nosso intervalo está igual ao erro, então podemos parar por aqui e dar como resposta a aproximação para a raiz x - = 0 . 64 16 .

Resposta

b k = 10

c x - = 0 . 6416

Exercício Resolvido #9

Lista 2 – Professora Juliana – UFRJ – Questão 2 – Item iv

Seja f x = e - x - x em 0,1 , faça:

a Mostre que f x é contínua no intervalo e teste se existe uma raiz no intervalo.

b Encontre o número de iterações k para uma precisão de ε = 10 - 3 usando o método da bisseção.

c Faça k iterações e forneça uma estimativa para a raiz.

Passo 1

a As funções e - x e x não possuem nenhuma descontinuidade no intervalo 0,1 , então nossa f x é contínua.

Para testar se tem uma raiz basta usarmos o teorema de Bolzano:

f 0 = 1

f 1 = 1 e - 1 ≅ - 0 . 632

Temos f 0 ∙ f 1 < 0 , logo existe uma raiz nesse intervalo.

Passo 2

b Agora para acharmos o número de iterações só jogarmos naquela fórmula:

k > ln ⁡ b 0 - a 0 - ln ⁡ ε ln ⁡ 2 = ln ⁡ 1 - ln ⁡ 0.001 ln ⁡ 2 ≅ 9.96 ⇒ k = 10

Beleza, precisamos de 10 iterações! Agora vamos aplicar nosso algoritmo!

Passo 3

c a 0 , b 0 = 0,1

ε = 0.001

Iteração 1 :

x 1 = a 0 + b 0 2 = 0.5

f x 1 = f 0.5 ≅ 0.11

f a 0 ∙ f x 1 = 1 ∙ 0.1 1 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 0.5,1

Critério de Parada:

b 1 - a 1 = 1 - 0.5 = 0.5 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 1 , b 1 = 0.5,1

ε = 0.001

Iteração 2 :

x 2 = a 1 + b 1 2 = 0.75

f x 2 = f 0.75 ≅ - 0.27

f a 1 ∙ f x 2 = 0.11 ∙ - 0.27 < 0

Logo, nosso novo intervalo será formado por a 1 e x 2 . Temos então que:

a 2 , b 2 = a 1 , x 2 = 0.5,0.75

Critério de Parada:

b 2 - a 2 = 0.75 - 0.5 = 0.25 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 0.5,0.75

ε = 0.001

Iteração 3 :

x 3 = a 2 + b 2 2 = 0.625

f x 3 = f 0.625 ≅ - 0.09

f a 2 ∙ f x 3 = 0.11 ∙ - 0.09 < 0

Logo, nosso novo intervalo será formado por a 2 e x 3 . Temos então que:

a 3 , b 3 = a 2 , x 3 = 0.5,0.625

Critério de Parada:

b 3 - a 3 = 0.625 - 0.5 = 0.125 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 0.5,0.625

ε = 0.001

Iteração 4 :

x 4 = a 3 + b 3 2 = 0.5625

f x 4 = f 0.5625 ≅ 0.007

f a 3 ∙ f x 4 = 0.11 ∙ 0.007 > 0

Logo, nosso novo intervalo será formado por x 4 e b 3 . Temos então que:

a 4 , b 4 = x 4 , b 3 = 0.5625 , 0.625

Critério de Parada:

b 4 - a 4 = 0.625 - 0.5625 = 0.0625 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 0.5625 , 0.625

ε = 0.001

Iteração 5 :

x 5 = a 4 + b 4 2 = 0.59375

f x 5 = f 0.59375 ≅ - 0.04

f a 4 ∙ f x 5 = 0.007 ∙ - 0.04 < 0

Logo, nosso novo intervalo será formado por a 4 e x 5 . Temos então que:

a 5 , b 5 = a 4 , x 5 = 0.5625 , 0.59375

Critério de Parada:

b 5 - a 5 = 0.59375 - 0.5625 = 0.03125 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 0.5625 , 0.59375

ε = 0.001

Iteração 6 :

x 6 = a 5 + b 5 2 = 0.578125

f x 6 = f 0.578125 ≅ - 0.017

f a 5 ∙ f x 6 = 0.007 ∙ - 0.017 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = 0.5625 , 0.578125

Critério de Parada:

b 6 - a 6 = 0.578125 - 0.5625 = 0.015625 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 6 , b 6 = 0.5625 , 0.578125

ε = 0.001

Iteração 7 :

x 7 = a 6 + b 6 2 = 0.5703

f x 7 = f 0.5703 ≅ - 0.005

f a 6 ∙ f x 7 = 0.007 ∙ - 0.005 < 0

Logo, nosso novo intervalo será formado por a 6 e x 7 . Temos então que:

a 7 , b 7 = a 6 , x 7 = 0.5625 , 0.5703

Critério de Parada:

b 7 - a 7 = 0.5703 - 0.5625 = 0.0078 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 7 , b 7 = 0.5625 , 0.5703

ε = 0.001

Iteração 8 :

x 8 = a 7 + b 7 2 = 0.5664

f x 8 = f 0.5664 ≅ 0.001

f a 7 ∙ f x 8 = 0.007 ∙ 0.001 > 0

Logo, nosso novo intervalo será formado por x 8 e b 7 . Temos então que:

a 8 , b 8 = x 8 , b 7 = 0.5664 , 0.5703

Critério de Parada:

b 8 - a 8 = 0.5703 - 0.5664 = 0.0039 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 8 , b 8 = 0.5664 , 0.5703

ε = 0.001

Iteração 9 :

x 9 = a 8 + b 8 2 = 0.5684

f x 9 = f 0.5683 ≅ - 0.002

f a 8 ∙ f x 9 = 0.001 ∙ - 0.00 2 < 0

Logo, nosso novo intervalo será formado por a 8 e x 9 . Temos então que:

a 9 , b 9 = a 8 , x 9 = 0.5664 , 0.5684

Critério de Parada:

b 9 - a 9 = 0.5684 - 0.5664 = 0.002 > 0.001

Como não alcançamos o critério de parada continuamos as iterações.

a 9 , b 9 = 0.5664 , 0.5684

ε = 0.001

Iteração 10 :

x 10 = a 9 + b 9 2 = 0.567 4

f x 10 = f 0.5673 ≅ - 0.0004

f a 9 ∙ f x 10 = 0.001 ∙ - 0.0004 < 0

Logo, nosso novo intervalo será formado por a 9 e x 10 . Temos então que:

a 10 , b 10 = a 9 , x 10 = 0.5664 , 0.567 4

Critério de Parada:

b 10 - a 10 = 0.567 4 - 0.56 6 4 = 0.001 = 0.001

Finalmente! Nosso intervalo está igual ao erro, então podemos parar por aqui e dar como resposta a aproximação para a raiz x - = 0.56 69 .

Resposta

b k = 10

c x - = 0.56 69

Exercício Resolvido #10

Lista de Exercícios – Módulo 4 – Professor Bruno Queiroz – UFCG – Questão 2

A velocidade de ascensão de um foguete em vôo vertical próximo a superfície terrestre v pode ser aproximada pela seguinte expressão:

v = u ∙ ln ⁡ M 0 M 0 - c ∙ t + g ∙ t

Na qual:

u : velocidade de exaustão relativa do foguete

M 0 : massa do foguete ao ser lançado

c : taxa de consumo de combustível

g : aceleração gravitacional

t : tempo (medido a partir do lançamento)

Considerando u = 200 m / s   , M 0 = 1600 k g , g = 9.8 m / s 2 e c = 27 k g / s , determinar o instante em que v = 100 m / s . Empregar o método da bisseção para determinar uma raiz aproximada para a equação, com intervalo inicial 6,8 e tolerância de 0.8 % . Explicite o erro relativo a cada iteração.

Passo 1

Eita cacete. Que negócio é esse de física? Achei que estávamos em cálculo numérico!

Haha, relaxa cara, essas letras todas são só pra te complicar! Vamos começar nos livrando delas substituindo todos os valores dados e igualando a velocidade a 100 :

v = u ∙ ln ⁡ M 0 M 0 - c ∙ t + g ∙ t

100 = 200 ∙ ln ⁡ 1600 1600 - 27 t + 9.8 t

Melhorou um pouco né? Agora é só uma equação, nada de foguetes haha. Mas ainda não podemos resolver isso usando bisseção né? Temos que dar uma mexida:

200 ∙ ln ⁡ 1600 1600 - 27 t + 9.8 t - 100 = 0

Opa, agora sim! Vai dar trabalho, mas pelo menos sabemos fazer haha. Só faltou um detalhe! Que negócio é aquele de 0.8 % ? E de erro relativo a cada iteração?? Então aqui ele está usando outro critério de parada! Ele quer que o erro relativo de uma iteração pra outra, dado por:

x k - x k - 1 x k

Seja menor que 0.8 % . Bom agora que já esclarecemos isso vamos partir em frente.

Passo 2

Ta pronto? Bebe uma água e toma coragem que esse é chatinho:

a 0 , b 0 = 6,8

ε = 0.008

Iteração 1 :

x 1 = a 0 + b 0 2 = 7

f x 1 = f 7 ≅ - 6.2 6

f a 0 ∙ f x 1 = - 19.84 ∙ - 6.2 6 > 0

Logo, nosso novo intervalo será formado por x 1 e b 0 . Temos então que:

a 1 , b 1 = x 1 , b 0 = 7,8

Critério de Parada:

Como não temos um chute inicial continuamos as iterações.

a 1 , b 1 = 7,8

ε = 0.00 8

Iteração 2 :

x 2 = a 1 + b 1 2 = 7.5

f x 2 = f 7.5 ≅ 0.56

f a 1 ∙ f x 2 = - 6.26 ∙ 0.56 < 0

Logo, nosso novo intervalo será formado por a 1 e x 2 . Temos então que:

a 2 , b 2 = a 1 , x 2 = 7,7.5

Critério de Parada:

x 2 - x 1 x 2 = 0.5 7.5 = 0.0667 > 0.008

Como não alcançamos o critério de parada continuamos as iterações.

a 2 , b 2 = 7,7.5

ε = 0.00 8

Iteração 3 :

x 3 = a 2 + b 2 2 = 7.25

f x 3 = f 7.25 ≅ - 2.85

f a 2 ∙ f x 3 = - 6.26 ∙ - 2.85 > 0

Logo, nosso novo intervalo será formado por x 3 e b 2 . Temos então que:

a 3 , b 3 = a 2 , x 3 = 7.25,7.5

Critério de Parada:

x 3 - x 2 x 3 = 0.25 7 . 25 = 0 . 0345 > 0.008

Como não alcançamos o critério de parada continuamos as iterações.

a 3 , b 3 = 7.25,7.5

ε = 0.00 8

Iteração 4 :

x 4 = a 3 + b 3 2 = 7.375

f x 4 = f 7.375 ≅ - 1.14

f a 3 ∙ f x 4 = - 2.8 5 ∙ - 1.14 > 0

Logo, nosso novo intervalo será formado por x 4 e b 3 . Temos então que:

a 4 , b 4 = x 4 , b 3 = 7.375 , 7.5

Critério de Parada:

x 4 - x 3 x 4 = 0 . 125 7.375 = 0.0 169 > 0.008

Como não alcançamos o critério de parada continuamos as iterações.

a 4 , b 4 = 7.375 , 7.5

ε = 0.00 8

Iteração 5 :

x 5 = a 4 + b 4 2 = 7.4375

f x 5 = f 7.4375 ≅ - 0.29

f a 4 ∙ f x 5 = - 1.14 ∙ - 0.29 > 0

Logo, nosso novo intervalo será formado por x 5 e b 4 . Temos então que:

a 5 , b 5 = x 5 , b 4 = 7.4375 , 7.5

Critério de Parada:

x 5 - x 4 x 5 = 0 . 0625 7.4375 = 0.0 084 > 0.008

Essa foi quase em haha. Mas como não alcançamos o critério de parada continuamos as iterações.

a 5 , b 5 = 7.4375 , 7.5

ε = 0.00 8

Iteração 6 :

x 6 = a 5 + b 5 2 = 7.46875

f x 6 = f 7.46875 ≅ 0.13

f a 5 ∙ f x 6 = - 0.29 ∙ 0.13 < 0

Logo, nosso novo intervalo será formado por a 5 e x 6 . Temos então que:

a 6 , b 6 = a 5 , x 6 = 7.4375 , 7.46875

Critério de Parada:

x 6 - x 5 x 6 = 0.03125 7.46875 = 0.00 42 < 0.008

Beleza! Nosso erro relativo está menor que a tolerância, então podemos parar por aqui e dar como resposta a aproximação para a raiz x - = 7.4531 .

Resposta

Instante t = 7.4531 segundos.

Erro relativo por iteração:

k = 1 :   -

k = 2 : 6 . 67 %

k = 3 : 3.45 %

k = 4 : 1.69 %

k = 5 : 0.84 %

k = 6 : 0.42 %

Exercícios de Livros Relacionados

Pelo Teorema do Valor Médio temos que x k + 1 - ξ = φ ' ( c k ) ( x k - ξ ) com c k entre x k e ξ . Analise os sinais de x j - ξ , j = 0,1 , . . .
Usando a regra de sinal de descartes, verifique que a equação p x = 3 x 5 - x 4 - x 3 + x + 1 = 0 pode ter duas raízes reais no intervalo.
Se no método da bissecção tomarmos sistematicamente x = a k + b k 2 , teremos que | x _ - ξ | ≤ b k - a k 2 .Considerando este fato:estime o número de iterações que o método efetuará;escreva um novo a
O método da bissecção pode ser aplicado sempre que f ( a ) f ( b )0 , mesmo que f ( x ) tenha mais que um zero em ( a ,b ) . Nos casos em que isto ocorre, verifique, com o auxílio de gráficos, se é po
Aplique o método da bissecção para resolver:a) 𝑒 𝑥 − 𝑥 − 3 𝑥 = 0 Obtendo em cada caso a e b (iniciais) graficamente.