Volumes de Sólidos Infinitos
Produzido por Arthur Melo de AlmeidaTeoria
Se tivermos uma região que queremos rotacionar, e essa região for limitada por essa curva que possui uma assíntota e um eixo, para calcular o volume do sólido gerado por essa rotação, teremos que utilizar integral imprópria.
A ideia é a mesma: a curva tende àquele eixo quando ou . Então um dos limites de integração será infinito.
Vou usar o mesmo exemplo que usei lá em áreas com integral imprópria.
Exemplo: Encontre o volume do sólido gerado pela rotação da região dada abaixo em torno do eixo .
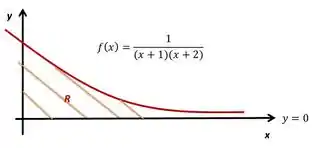
Lembra que para um sólido de rotação em torno do eixo , o volume é definido por:
O raio é a distância entre a curva e o eixo de rotação e e são os limites de integração. Nesse caso, como o eixo de rotação é o próprio eixo , então o raio será . Além disso, nesse caso, será .
Pronto. Então temos assim:
Vamos resolver a primitiva e depois encontrar os limites:
Frações parciais... É aquele caso em que todos os termos do denominador são lineares mas se repetem, lembra?
Para
Para
Para
Para
Multiplicando a equação por :
Resolvendo o sistema:
Somando as duas equações
Sendo assim:
Essas duas integrais que restaram saem por substituição simples:
Por fim:
Aplicando o Teorema Fundamental do Cálculo:
Aplicando o limite:
E por fim, chegamos no volume:
1 x + 1 2 x + 2 2 = A x + 1 + B x + 1 2 + C x + 2 + D x + 2 2
1 x + 1 2 x + 2 2 = - 2 x + 1 + 1 x + 1 2 + 2 x + 2 + 1 x + 2 2
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ - Cálculo 1 - PF 2014.2 – 2
Calcule o volume do sólido de revolução obtido pela rotação da curva
Em torno do eixo .
Passo 1
Cara, essa função é estranhíssima, não vou perder tempo tentando fazer seu desenho. Agora, eu sei que estou girando em torno do eixo , então vou usar o método das seções transversais torcendo que esse método realmente resolva numa integral que não seja impossível de ser feita:
Tem que se ligar agora em duas coisas: que essa integral é imprópria; e que a derivada de é um múltiplo de . Ué, e por que eu disse isso?
Essa substituição vai simplificar bastante a nossa integral! Mas não pode esquecer de mudar os limites de integração também:
Passo 2
Resolvendo esse cara, olha como fica:
Resposta
Exercício Resolvido #2
Elaboração própria
Tendo em vista a área entras as funções abaixo:
Calcule o volume do sólido obtido na rotação dessa região em torno do eixo .
Passo 1
Plotei o negócio todo, agora vamos olhar qual é a região:
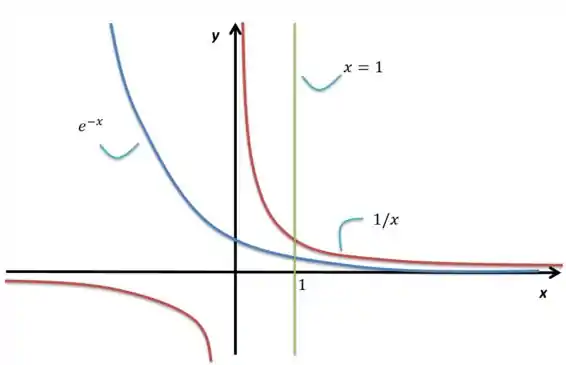
Se você reparar, não existe uma área perfeitamente definida. Olha o que acontece, antes do você tem uma região na qual os gráficos vermelho e azul vão se separando e não tem um “teto” para fechar essa área. Indo para o outro lado, os dois gráficos também não são limitados por uma parede, mas pelo menos eles estão se encostando, diminuindo a área.
O que faremos nesse caso? Vamos calcular o volume de rotação de uma área ilimitada!
Bizarro, eu sei. Não faz nenhum sentido a primeira vista, mas matematicamente é perfeitamente normal. O detalhe é que vamos cair em uma amada integral imprópria.
Passo 2
Bom, se essa área roda em torno de , podemos defini-la assim:
Agora, é só resolver!
Só te recordando, como a integral é imprópria, eu devo fazer um limite para o infinito de uma variável que eu colocarei no lugar do limite superior.
As duas funções de ali vão ficando pequenas no infinito. Ambas tendem a (basta substituir o valor para ter uma noção). Dessa forma, o resultado é aquilo que sobrou de constante:
Resposta
Exercício Resolvido #3
UNICAMP - Cálculo 1 - Exame 2012 Diurno - 5 b
Ao rotacionarmos em torno do eixo a região delimitada pela função , obtemos um sólido conhecido por Trombeta de Gabriel. No entando, ao girarmos em torno do eixo , obtemos um outro sólido conhecido como Vulcão de Descartes.
Calcule o volume do Vulcão de Descartes, para suficientemente grande, ou seja, .
Passo 1
Nosso esboço é o mesmo da última questão para um qualquer.
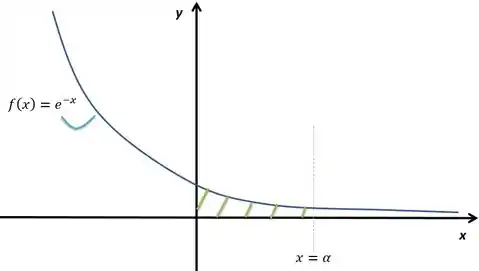
Rotacionando em torno do eixo nós teríamos o seguinte, pelo método das cascas cilíndricas:
Vamos resolver essa integral para um qualquer e depois fazemos ele tender a .
Passo 2
Vamos com a integral por partes. Pelo LIATE, a o e o :
Ok, agora calculamos o limite disso aí quando vai a .
Passo 3
Substituindo esse limite aí a gente cai numa indeterminação . Vamos de L’Hospital então:
Esse é o volume que estávamos procurando!