Integral de Linha de Campos Vetoriais no Espaço
Produzido por Arthur Melo de AlmeidaTeoria
Introdução
Nós sabemos que para calcular o trabalho de uma força em uma curva no plano, podemos fazer:
Onde é um campo vetorial na forma e é o vetor tangente a curva parametrizada em . E o que calculamos é, justamente, a integral do produto escalar entre eles.
Mas, assim como no caso escalar, uma integral de linha vetorial não está limitada para o plano e, portanto, podemos extender o conceito de trabalho como uma integral de linha para qualquer curva no espaço.
Não deve ser nada muito surpreendente, mas vamos ver como. Haha
Definição
Como aqui estamos trabalhando com três dimensões, nosso campo não será mais , mas . Nada muito diferente.
O vetor tangente também terá três componentes, para que possamos fazer o produto escalar direito.
E juntando as coisas, temos:
Ou, também:
Quase igual, né? Achou que não mudou nada?
Então vou te mostrar um exemplo pra você ver onde que fica a dificuldade. Mas fica calma que a gente vai fazer o passo-a-passo e você vai entender tudo direitinho.
Exemplo
Calcule , onde e é a curva que parametriza a interseção de com o plano , percorrida no sentido anti-horário.
Passo 1: Montar o problema
Vamos utilizar a fórmula
Temos o campo, mas não a parametrização, então vamos encontrá-la.
Passo 2: encontrar a parametrização da curva
Repare que se jogarmos a equação do plano na outra superfície, vamos ter que a projeção da curva no plano é a circunferência:
Portanto, a parametrização da projeção de no plano é dada, em coordenadas polares deslocadas, por:
Mas é uma curva em três dimensões, tá faltando a coordenada , que é dada pela equação do plano
Então, uma parametrização de seria:
E, para termos sentido anti-horário, vamos ter que o parâmetro vai ser dado de a .
Passo 3: calcular
Passo 4: Substituir tudo na integral e escrever em função de
O campo é dado por
Aplicando a parametrização, temos
Substituindo então na integral, temos
Passo 5: calcular a integral
Lembrando que
Entendeu? Fica bem mais extenso, né? Mas nada que se tenha que quebrar a cabeça demais, é bom só estar ligado para não se perder entre os passos e conseguir se organizar, porque é muita informação, muita conta e tal...
Mas isso se ganha com a prática, vamos aos exercícios!
Exercícios Resolvidos
Exercício Resolvido #1
CEFET - Cálculo Vetorial - Lista 1 Thomé – 10
Calcule a integral de linha , onde é a fronteira da parte do plano no primeiro octante.
Passo 1
A gente viu na teoria que para calcular um integral de linha, podemos usar a fórmula:
Nós já temos o campo, que vai ser , então só falta parametrizar a curva e encontrar o vetor tangente. Vamos lá!
Passo 2
Ele diz que nossa curva é a fronteira de um plano, então vamos ver qual é essa figura que ele está falando:
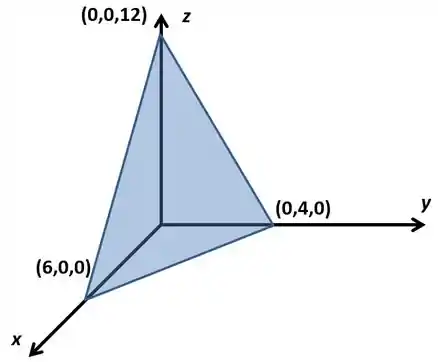
Na real, nossa curva é o contorno desse triângulo. Então, é a união de 3 segmentos de reta, consequentemente
Passo 3
Mas que segmentos de retas são esses? Olha os pontos onde o plano corta os eixos, vamos ver quando ele corta o eixo , ou seja, quando
Ele passa no ponto
Vamos ver quando ele corta o eixo , ou seja, quando
Ele passa no ponto
Vamos ver quando ele passa no eixo , ou seja, quando
Ele passa no ponto
Vamos fazer a curva sendo a curva do plano quando . A curva sendo a curva do plano quando . A curva sendo a curva do plano quando . Temos que ficar atentos em cada parte para ver a orientação, vamos fazer no sentido anti-horário, ou seja, de até até
Passo 4
Vamos começar com a curva
Precisamos parametrizar esse segmento de reta. Basta pegar a equação do plano e trocar
Vamos isolar o porque é o que aumenta quando vai de até
Então, fazendo , vamos ter
Com indo de à , tendo
Passo 5
Agora calculamos :
Passo 6
Vamos, agora, utilizar a fórmula, substituindo o valor de e escrevendo em função de :
Passo 7
Vamos ver a segunda agora
Precisamos parametrizar esse segmento de reta. Basta pegar a equação do plano e trocar
Vamos isolar o porque é o que aumenta quando vai de até
Fazendo :
Com indo de à , tendo
Passo 8
Agora calculamos :
Passo 9
Vamos, agora, utilizar a fórmula, substituindo o valor de e escrevendo em função de :
Nossa, quanta conta... Mas não perde o ânimo não que só falta uma!
Passo 10
Vamos ver a terceira agora
Precisamos parametrizar esse segmento de reta. Basta pegar a equação do plano e trocar
Vamos isolar o porque é o que aumenta quando vai de até
De novo, vamos fazer :
Com indo de à , tendo
Passo 11
Agora calculamos :
Passo 12
Vamos, agora, utilizar a fórmula, substituindo o valor de e escrevendo em função de :
Passo 13
Finalmente, agora que temos as integrais, é só substituir
Resposta
Exercício Resolvido #2
George B. Thomas, Cálculo – volume 2, 11ª edição, São Paulo: Pearson Education do Brasil, 2009, pp. 485-43.
O campo é o campo de velocidades de um escoamento no espaço. Encontre o escoamento de até ao longo da curva de interseção do cilindro e do plano . (Sugestão: use como parâmetro.)
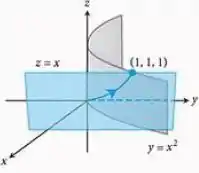
Passo 1
Na teoria a gente viu que escoamento nada mais é que a integral de linha:
O campo foi dado no enunciado , só fica faltando a parametrização da curva .
Então vamos começar por isso, né?
Passo 2
O exercício da uma dica boa de usar , então vamos usá-la. E isso dá que , certo?
Então, pelo cilindro, encontramos que a projeção no plano pode ser parametrizada por:
Mas aqui estamos no , então vamos usar a outra superfície para encontrar a parametrização da nossa curva no espaço.
E o que temos é algo simples, o plano , que nos dá também.
Assim temos que nossa curva tem parametrização:
Que vai de a , então , concorda?
Passo 3
Da parametrização podemos tirar o vetor tangente:
E agora já temos tudo que precisamos pra calcular a integral, é so jogar na fórmula!
Passo 4
Então, vamos ter que:
Resposta
Exercício Resolvido #3
UFF - Cálculo IIIA - Lista 4 - 6
Seja a interseção do cilindro com o semiplano , , percorrida de modo que sua projeção no plano tenha sentido anti-horário e seja . Calcule a integral
Passo 1
Na teoria vimos que a integral de linha é dada por:
O campo foi dado no enunciado só fica faltando a parametrização da curva. Então vamos atrás dela!
Passo 2
Precisamos conseguir parametrizar a curva . Podemos parametrizar o cilindro direto
Vamos ter
Ele disse que isso nos diz que
Então
Falta a componente , mas temos uma relação entre e
Então
Vamos ter
Com
Passo 3
Agora calculamos
Passo 4
Uma coisa que temos que ficar atentos na integral de linha é o sentido da curva. Ele disse que o sentido é anti-horário da projeção no plano , isso já é a orientação normal que temos, e estamos rodando no sentido anti-horário.
Vamos, então, substituir e na integral.
Vamos resolver essa integral separada
Passo 5
Vamos fazer
Então
A integral vai ficar
Resolvendo a integral vamos ter
Voltando para
Passo 6
Voltando para nossa integral
Vamos ter
Resposta
Exercício Resolvido #4
UFF - Cálculo IIIA - Lista 4 - 5a
Calcule
Onde e é a interseção das superfícies e , percorrida no senti anti-horário quando vista da origem.
Passo 1
Vamos usar a fórmula que vimos na teoria pra integrais de linha vetoriais:
O campo foi dado no enunciado, então só falta parametrizarmos a cruva e encontrarmos o vetor tangente. Vamos ver como que fica!
Passo 2
Precisamos conseguir parametrizar a curva , primeiro vamos achar a interseção entre as duas superfícies, fazendo
Substituindo na equação da esfera
Vamos completar quadrados agora
Isso é uma elipse, vamos parametrizar essa elipse, vamos ter
Com
Falta a componente , mas temos uma relação entre e
Então
Vamos ter
Com
Passo 3
Agora calculamos
Passo 4
Mas uma coisa que temos que ficar atentos na integral de linha é o sentido do cara. Ele disse que o sentido é anti-horário quando visto da origem, isso quer dizer que, para o nosso sentido “normal”, ele roda ao contrário do visto pela origem, ou seja, neste caso vai ser no sentido horário.
Mas a nossa parametrização foi feita para a curva percorrendo o sentido anti-horário, com orientaçao positiva. Para corrigir isso, ao invés de integrarmos sobre , vamos integrar sobre , de forma que:
Agora é só jofgar tudo na integral e calcular!
Passo 5
Vamos, então, substituir e na integral.
Lembrando que
A integral vai ficar