Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Fluxo em Curvas

Ver Todos os Exercícios

Teoria

Introdução

Até agora, vimos Integrais de linha vetoriais usadas para cálculos de trabalho, circulação e escoamento.

Agora vamos ver mais um tipo de aplicação para integrais de linha, mas que não se encaixa na definição anterior: Integrais de Fluxo.

Fisicamente, o fluxo pode ser entendido como a taxa que o fluído “sai” ou “entra” em uma região delimitada por uma curva fechada. Mas também podemos aplicar essa integral para qualquer campo vetorial, como os que temos trabalhado até agora.

Como queremos medir a taxa de entrada e saída, dessa vez usaremos o vetor normal a curva, diferentemente das outras integrais de linha, que usavamos o vetor tangente σ → ' t , lembra?

Então, se tinhamos:

T r a b a l h o = ∫ a b F → ∙ σ → ' d t

Vamos ter agora:

F l u x o = ∫ a b F → ∙ n →   d t

É bem parecido, só precisamos ver como encontrar esse tal vetor normal, né?

Vamos te mostrar, então!

Vetor Normal

O vetor normal é um vetor perpendicular ao vetor tangente que vimos antes, então vamos começar relembrando o tangente:

σ → ' = d x d t , d y d t

Pra quem não lembra, ou nunca viu, um macete pra encontrar vetores perpendiculares é trocar as componentes e trocar o sinal de uma delas. Então n → é algo assim:

n → = d y d t , - d x d t   o u   - d y d t , d x d t

Vamos ver rapidinho que ele realmente é perpendicular ao vetor σ → ' . Para isso, vamos fazer o produto escalar entre σ → ' e n → e ver que ele vai dar zero.

σ → ' ∙ n → = d x d t , d y d t ∙ d y d t , - d x d t = d x d t d y d t - d y d t d x d t = 0

Beleza, eles realmente são perpendiculares, e esse é realmente o vetor normal =D

Mas e agora, qual escolher?

Se sua curva andar no sentido anti-horário:

n → = d y d t , - d x d t

Se tiver no sentido horário:

n → = - d y d t , d x d t

Como que você vai lembrar disso? Vê a primeira componente do vetor, com orientação positiva (anti-horário) temos d y d t ; orientação negativa (horário) temos - d y d t . Não vai se confundir, hein?

Notação

Assim como a integral de trabalho podia ser escrita como:

∫ a b F → ∙ σ → ' d t = ∫ C F 1 d x + F 2 d y

Também temos uma notação parecida se fizermos:

∫ a b F → ∙ n →   d t = ∫ a b F 1 , F 2 ∙ d y d t , - d x d t d t = ∫ C F 1 d y - F 2 d x

Uma forma que você pode pensar é que, na fórmula do fluxo, vamos ter o nosso campo vetorial da integral de linha, sendo na verdade:

F → f l u x o x , y = - F 2 , F 1

Então, na verdade, fazemos a integral de linha vetorial usando essa F → f l u x o . Ou seja,

∫ a b F → ∙ n →   d t = ∫ a b F → f l u x o ∙ σ → '   d t = ∫ C - F 2 d x + F 1 d y

Vamos fazer um exemplo disso para entender bem?

Exemplo

Calcule o fluxo do campo

F → = x   i → + y   j →

Através da curva

C : σ → = cos ⁡ t , sen ⁡ t ,   0 ≤ t ≤ 2 π

Passo 1: Montar o problema

Se ele quer o fluxo pela curva, então, na verdade o que queremos é:

∫ a b F → ∙ n →   d t

Que já temos a parametrização da curva e o campo, só falta o vetor normal.

Passo 2: Encontrar o vetor normal

O vetor normal é dado por:

n → = d y d t , - d x d t = ( cos ⁡ t , sin ⁡ t )

E agora é so jogar tudo na integral!

Passo 3: Calcular a integral

Agora que já temos tudo, podemos fazer:

∫ a b F → ∙ n →   d t = ∫ 0 2 π cos ⁡ t , sin ⁡ t ∙ cos ⁡ t , sin ⁡ t d t

= ∫ 0 2 π cos 2 ⁡ t + sin 2 ⁡ t d t = ∫ 0 2 π 1 d t = t │ 0 2 π = 2 π

Resumindo o passo-a-passo:

Passo 1: Montar o problema

Passo 2: Encontrar o vetor normal

Passo 3: Calcular a integral

Mas agora vamos ver uns exercícios pra fixar mesmo essa ideia!

Vetor Normal

Notação

Exercícios Resolvidos

Exercício Resolvido #1

UNICAMP - Cálculo 2 - P3 2010 Manhã - 1b

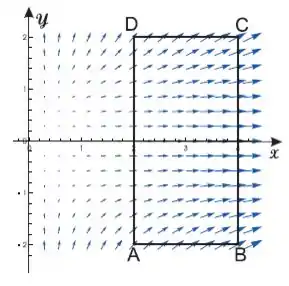
Considere um campo de vetores G ( x , y ) e uma curva C , fechada, de forma retangular, como na figura abaixo. Analise o sinal da integral de linha ∫ G . n d t ( n é o versor normal exterior) sobre cada um dos segmentos de C . O fluxo de G sobre C é positivo ou negativo? Justifique as respostas.

Passo 1

Essa questão é resolvida basicamente pelos conceitos de produto escalar. Nós queremos saber o sinal da integral de linha

∫ G ⋅ n d t

Então onde o produto G ⋅ n for negativo a integral será negativa e onde for positivo será positivo. Vamos analisar cada segmento separadamente.

Passo 2

Vamos começar com o segmento C B .

Se a curva está orientada com a normal n apontando para fora e, nesse trecho, o campo G (como vemos pela figura) tem a mesma direção e sentido de n , sabemos que o produto escalar é positivo.

Em outras palavras: a projeção do campo na direção de n tem o mesmo sentido de n , portanto, o fluxo é positivo.

Seguindo esse mesmo raciocínio para o trecho A D , temos o resultado oposto: o fluxo é negativo. Isso porque a projeção do campo na direção de n tem sentido oposto a n .

Passo 3

Em resumo: a orientação positiva de C é com a normal para fora, logo, onde o campo “sai”, a integral ∫ G . n d t é positiva, onde ele “entra” é negativa.

Em A B e D A é negativo e B C e C D   positivo.

∫ A B G ∙ n   d t   < 0

∫ D A G ∙ n   d t < 0

∫ B C G ∙ n   d t > 0

∫ C D G ∙ n   d t > 0

Passo 4

Agora vamos analisar o fluxo total na curva fechada C . Sabemos que em dois trechos o fluxo é positivo e em outros 2 negativo, mas isso não quer dizer que o total é zero!

Esses fluxos tem valores diferentes, dependendo do tamanho do vetor do campo no trecho.

Se você reparar, nos trechos A B e C D o campo tem o mesmo módulo, ou seja, seus vetores têm o mesmo tamanho. Portanto, os valores absolutos das integrais são os mesmos, porém, com sinal contrário. Assim, temos:

∫ A B G ∙ n   d t + ∫ C D G ∙ n   d t = 0

Passo 5

Agora vamos ver os trechos A D e B C . O primeiro tem fluxo negativo e o segundo, positivo, sendo que o campo tem módulo maior no segundo. Portanto, podemos escrever:

∫ D A G ∙ n   d t + ∫ B C G ∙ n   d t > 0

Passo 6

Sobre o fluxo total temos:

ϕ f l u x o C = ∫ A B G ∙ n   d t + ∫ C D G ∙ n   d t ⏟ 0 + ∫ D A G ∙ n   d t + ∫ B C G ∙ n   d t

ϕ C = ∫ D A G ∙ n   d t + ∫ B C G ∙ n   d t > 0

Logo, o fluxo total é positivo.

Resposta

∫ A B G ∙ n   d t   < 0

∫ D A G ∙ n   d t < 0

∫ B C G ∙ n   d t > 0

∫ C D G ∙ n   d t > 0

ϕ f l u x o C > 0

Exercício Resolvido #2

George B. Thomas, Cálculo – volume 2, 11ª edição, São Paulo: Pearson Education do Brasil ltda., 2009, pp. 484-30.

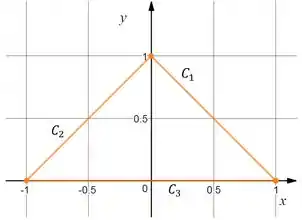
Encontre o fluxo exterior do campo

F = x + y i - x 2 + y 2 j

Através do triângulo de vértices ( 1,0 ) , ( 0,1 ) , ( - 1,0 ) .

Passo 1

O que o exercício pede é o fluxo, que como vimos na teoria, podemos calcular por:

∫ γ F → ∙ n →   d t

Mas a nossa curva γ é um triângulo, composto de 3 retas, de forma que:

γ = C 1 ∪ C 2 ∪ C 3

E por isso:

∫ γ F → ∙ n →   d t = ∫ C 1 F → ∙ n →   d t + ∫ C 2 F → ∙ n →   d t + ∫ C 3 F → ∙ n →   d t

Então vamos calcular uma por uma pra ficar bem organizado!

Passo 2

Vamos começar por C 1 , que é a reta que vai de ( 1,0 ) a ( 0,1 ) , parametrizada por:

C 1 : σ → = 1 - t ,   t   ,   0 ≤ t ≤ 1

Lembramos que para encontrar o vetor normal, fazemos:

n → = d y d t , - d x d t = ( 1,1 )

E jogamos na integral:

∫ C 1 F → ∙ n →   d t = ∫ 0 1 1 - t + t ,   - 1 - t 2 + t 2 ∙ 1,1   d t

= ∫ 0 1 1 - 1 + 2 t - 2 t 2 d t = t 2 │ 0 1 - 2 t 3 3 │ 0 1

= 1 - 2 3 = 1 3

Até agora tudo bem, vamos ver a próxima!

Passo 3

Vamos repetir as contas, mas agora pra C 2 , que é a reta de ( 0,1 ) a ( - 1,0 ) , com parametrização:

C 2 : σ → = - t ,   1 - t   ,   0 ≤ t ≤ 1

E o vetor normal a gente acha da mesma forma:

n → = d y d t , - d x d t = ( - 1,1 )

Então jogamos na integral de novo:

∫ C 2 F → ∙ n →   d t = ∫ 0 1 - t + 1 - t ,   - - t 2 + 1 - t 2 ∙ - 1,1   d t

= ∫ 0 1 2 t - 1 - 1 + 2 t - 2 t 2 d t = ∫ 0 1 - 2 + 4 t - 2 t 2   d t

= - 2 t │ 0 1 + 2 t 2 │ 0 1 - 2 t 3 3 │ 0 1 = - 2 + 2 - 2 3 = - 2 3

Só mais uma agora, vamos lá!

Passo 4

Pra fechar, temos que C 3 é a reta ligando ( - 1,0 ) a ( 1,0 ) , que podemos parametrizar assim:

C 3 : σ → = t ,   0 ,     - 1 ≤ t ≤ 1

De novo, vamos ter o vetor normal:

n → = d y d t , - d x d t = ( 0 , - 1 )

E é só jogar na integral:

∫ C 3 F → ∙ n →   d t = ∫ - 1 1 t + 0 , - t 2 + 0 2 ∙ 0 , - 1   d t

= ∫ - 1 1 t , - t 2 0 , - 1 d t = ∫ - 1 1 t 2 d t = t 3 3 - 1 1 =

= 1 3 + 1 3 = 2 3

Pronto, agora é só somar tudo pra termos o resultado final!

Passo 5

Lembrando que gente tinha:

∫ γ F → ∙ n →   d t = ∫ C 1 F → ∙ n →   d t + ∫ C 2 F → ∙ n →   d t + ∫ C 3 F → ∙ n →   d t

Então o fluxo exterior ao triângulo vai ser:

∫ γ F → ∙ n →   d t = 1 3 - 2 3 + 2 3 = 1 3

Nada tão bizarro assim, só um pouquinho trabalhoso, né? Mas agora já foi, o que importa é que resolvemos a questão. haha

Resposta

1 3

Exercício Resolvido #3

Hamilton Luiz Guidorizzi, Um Curso de Cálculo – volume 3, 5ª edição, Rio de Janeiro: LTC, 2002, pp. 203-3.

Seja

F → x , y = x x 2 + y 2 5 i → + y x 2 + y 2 5 j →

E n → a normal unitária exterior ao círculo x 2 + y 2 ≤ 1 . Calcule ∫ γ F → ∙ n →   d t onde γ = ( cos ⁡ t , sin ⁡ t ) , 0 ≤ t ≤ π .

Passo 1

O que a questão está pedindo uma integral de linha:

∫ γ F → ∙ n →   d t

Onde n → é o vetor normal a curva.

Passo 2

Pra começar, vemos que γ é a paramentrização do círculo dado na questão (ou pelo menos parte dele, já que t só vai até π ). Já é um bom sinal!

Só falta verificar se o vetor normal a γ também é unitário.

Vamos lembrar que o vetor normal a curva pode ser obtido por:

n → γ = d y d t ,   - d x d t = cos ⁡ t , sin ⁡ t

Que tem módulo:

n → γ = cos ⁡ t 2 + sin ⁡ t 2 = 1

Ou seja, n → γ é unitário também e, portanto, é igual ao vetor n → dado na questão.

Passo 3

Só pra deixar organizado, vamos escrever o campo em função da parametrização:

F → x t , y t = cos ⁡ t cos 2 ⁡ t + + sin 2 ⁡ t 5   , sin ⁡ t cos 2 ⁡ t + + sin 2 ⁡ t 5 = cos ⁡ t , sin ⁡ t

Muito prático, nada muito complicado comparado ao que tinhamos antes, né?

Agora que já temos tudo que precisamos, só precisamos jogar na integral:

∫ γ F → ∙ n →   d t = ∫ 0 π cos ⁡ t , sin ⁡ t ∙ cos ⁡ t , sin ⁡ t   d t

= ∫ 0 π cos 2 ⁡ t + sin 2 ⁡ t d t = ∫ 0 π d t = t │ 0 π = π

Resposta

π

Exercícios de Livros Relacionados

2. Prove que F → . n → for constante sobre Im γ, então o fluxo deF → . n → através de γ é o produto de F → . n → pelo comprimento de γ, onde n → é normal a γ
Calcule ∫ γ F → . n → d s sendo dados ( para evitar repetição ficara subentendido que n → é unitário ) F → x , y = xi →+ yj →, γ t = t ,t 2 , 0 ≤ t ≤ 1 n → a normal com componente y0
Dentre todas as regiões retangulares 0 ≤ x ≤ a ,0 ≤ y ≤ b , encontre aquela para a qual o fluxo exterior total de F = x 2 + 4 x y i - 6 y j atraves dos quatro lados é minimo. Qual é o fluxo minimo?
Encontre uma equação para o plano através da origem de modo que a circulação do campo de escoamento F = z i + x j + y k ao redor da circunferência de interseção do plano com a esfera x 2 + y 2 + z 2 =
Massa de um fio Encontre a massa de um fio que se encontra ao longo da curva r(t) = (t2 – 1)j + 2tk, 0 ≤ t ≤ 1, se adensidade for d = (3/2)t