Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Integrais Duplas - Teorema de Fubini

Ver Todos os Exercícios

Teoria

Estamos sempre aprendendo novas coisas na matéria de Cálculo, e agora você está prestes a mergulhar em um novo assunto, o mundo das Integrais Duplas.

A integral dupla, nada mais é que um integral, dentro de outra integral, o que na pratica, só dobra o nosso trabalho, já que temos que calcular duas integrais, e não só uma! Mas muitas vezes você vai ver que em provas, os professores acabam pegando mais leve nas questões que envolvem integrais duplas, exatamente por causa desse "trabalho extra".

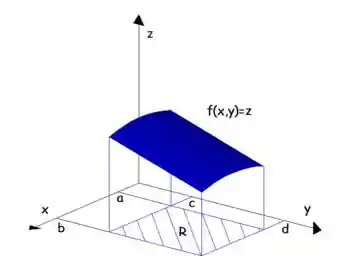
O mais interessante desse mundo de Integrais Duplas, é que agora começaremos a ver superfícies no , ou seja, conseguiremos desenhar superfícies e calcular o seu volume, utilizando integrais duplas. Nessa página estaremos interessados primeiramente nas regiões retangulares como essa, dá uma olhada:

Nesse mundo de Integrais Duplas muitas das nossas funções, serão funções de duas variáveis, como podemos ver na figura em que a região retangular é definida por . Esquecendo um pouco a forma da figura, quero que você olhe para a sombra dela no plano e repare que a região , tem formato de retângulo e tem seus limites definidos entre e , e entre e , certo?

Show, então caso a gente calculasse a a integral dupla da função :

Nós estaríamos calculando exatamente o volume da região que fica abaixo da superfície desenhado por . Essa é a interpretação geométrica de uma integral dupla.

As integrais duplas obedecem a algumas propriedades importantes, observe:

Linearidade

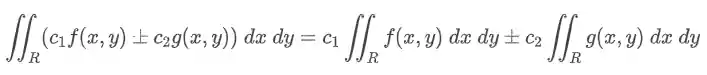
Monotonicidade

Se existem duas funções e tal que g para todo , então:

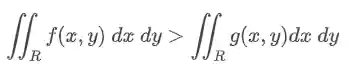
Aditividade

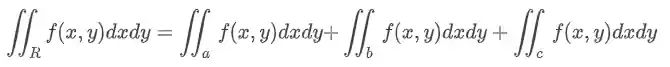
Podemos dividir uma região em várias subdivisões e reescrever a região somando essas subdivisões, se dividiom nas regiões , e , por exemplo:

Teorema de Fubini

O Teorema de Fubini, entra em cena quando desejamos calcular o valor de integrais duplas iteradas, ou seja, quando essas integrais possuem limites de integração bem definidos. Ele define uma maneira de transformar as integrais duplas em duas integrais simples, que nós já sabemos como calcular.

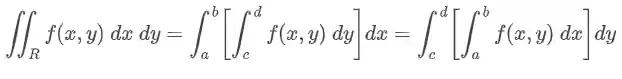
O Teorema de Fubini, diz que se temos uma função que define uma superfície contínua e uma região (como vimos no exemplo da figura), então:

Repare que a ordem que vamos calcular não importa, o que importa é que existe uma integral em relação a variável com o limite e uma integral em relação a variável com o limite .

Vamos fazer um exemplo, com nossa resolução Passo a Passo para você não ficar com dúvida na questão:

Exercício

Sendo , calcule o volume, de dentro da região .

Passo 1

A primeira coisa que temos que entender nessa questão é que teremos que calcular uma integral dupla da função , com os limites de integração definidos pela região formada no plano :

Passo 2

Agora vamos levar em consideração que os limites de integração em relação a são e que os limites de integração em relação a são , dessa forma:

Passo 3

Calculando a integral em relação a :

Que é o mesmo que:

Passo 4

Calculando agora a integral em relação a :

Passo 5

Portanto o volume dessa região , é de 20 unidades de volume.

Resposta

Teorema de Fubini

Exercício

Exercícios Resolvidos

Exercício Resolvido #1

James Stewart, Cálculo Vol. 2, tradução da 6ª ed. Norte-americana, Rio de Janeiro: CENGAGE learning, 2010, pp. 915

Calcule o valor da integral dupla

∬ R   x - 3 y 2   d A ,

onde R = { ( x , y ) | 0 ≤ x ≤ 2 ,   1 ≤ y ≤ 2 } .

Passo 1

Vamos desmembrar a integral utilizando o Teorema de Fubini.

∬ R   x - 3 y 2   d A = ∫ 1 2 ∫ 0 2 x - 3 y 2 d x   d y

Note que o intervalo da integral de fora está de acordo com d y e o da de dentro, com d x . E se você quisesse integrar ao contrário? Sem problemas, basta o intervalo estar de acordo:

∫ 0 2 ∫ 1 2 x - 3 y 2 d y   d x

Você encontrará o mesmo valor! Nesse exercício, vamos optar pela 1ª opção.

Passo 2

Agora você deve integrar em relação a x ,   ou seja, resolver a integral de dentro (tomando y como constante).

∫ 1 2 ∫ 0 2 x - 3 y 2   d x d y

∫ 0 2 x - 3 y 2 d x =

=   x 2 2 - 3 x y 2 x = 0 x = 2 =

= 4 2 - 3 2 y 2 - 0 =

= 2 - 6 y 2

Passo 3

Devemos, então, integrar em relação a y , substituindo o valor que encontramos no passo 2.

∫ 1 2   2 - 6 y 2   d y =

= 2 y - 6 y 3 3 y = 1 y = 2 =

= 2 2 - 2 ( 8 ) - 2 ( 1 ) - 2 ( 1 )   =

= 4 - 16 - 2 - 2 = - 12

Resposta

- 12

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2004, pp. 164

Calcule

∬ R   x sen ⁡ y - y e x   d x   d y

onde R = - 1,1 × [ 0 , π / 2 ] .

Passo 1

A primeira coisa a entender direitinho é esse retângulo R , ele deu dois intervalos, o primeiro em x e o segundo em y , a ordem é sempre essa não esqueça disso.

x ∈ - 1,1

y ∈ 0 , π 2

Vamos separar a integral dupla em integrais iteradas:

∫ 0 π / 2   ∫ - 1 1 x sen ⁡ y - y e x   d x   d y

Passo 2

Agora, vamos calcular a integral de dentro em relação a x (lembre-se, tome y como constante!)

∫ 0 π 2   ∫ - 1 1 x sen ⁡ y - y e x   d x d y =

∫ - 1 1 x sen ⁡ y - y e x   d x

= x 2 2 s e n   y - y e x - 1 1

= 1 2 sen ⁡ y - y e - 1 2 sen ⁡ y - y e

= - y e + y e

Passo 3

Integraremos, então, em relação a y :

∫ 0 π 2   - y e + y e   d y

= - e y 2 2 + y 2 2 e y = 0 y = π 2 =

= 1 2 - e π 2 4 + π 2 4 e - 0 =

Resposta

π 2 8 - e + 1 e

Exercício Resolvido #3

Howard Anton, Irl Bivens, Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: ARTMED EDITORA S.A, 2005, pag 1035-59.

Calcule

∬ R   x y 2 d A

na região R mostrada na figura abaixo,

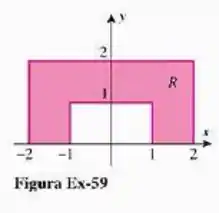
Passo 1

Bem, vamos começar escrevendo essa região, ok? Para isso, vamos dividí-la em 3 partes:

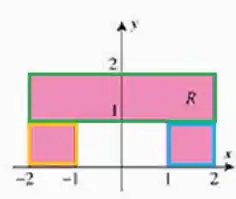
Chamando o retângulo verde de R 1 , o amarelo de R 2 e o azul de R 3 , temos o seguinte:

∬ R   x y 2 d A = ∬ R 1   x y 2 d A + ∬ R 2   x y 2 d A + ∬ R 3   x y 2 d A

Passo 2

Agora, vamos encontrar os inter valos de cada integral.

Para o retângulo verde, temos:

- 2 ≤ x ≤ 2 ;             1 ≤ y ≤ 2

Para o amarelo:

- 2 ≤ x ≤ - 1 ;             0 ≤ y ≤ 1

Para o azul:

1 ≤ x ≤ 2 ;             0 ≤ y ≤ 1

Passo 3

Aplicando o Teorema de Fubini, temos:

∬ R   x y 2 d A = ∫ 1 2 ∫ - 2 2 x y 2 d x d y + ∫ 0 1 ∫ - 2 - 1 x y 2 d x d y + ∫ 0 1 ∫ 1 2 x y 2 d x d y

Repare que a ordem dos intervalos está de acordo com a ordem dos diferenciais!

Passo 4

Agora, vamos resolver a integral de R 1 :

∬ R 1   x y 2 d A = ∫ 1 2 ∫ - 2 2 x y 2 d x d y

∬ R 1   x y 2 d A = ∫ 1 2 x 2 2 y 2 x = - 2 x = 2 d y + ∫ 0 1 x 2 2 y 2 x = - 2 x = - 1 d y + ∫ 0 1 x 2 2 y 2 x = 1 x = 2 d y

∬ R 1   x y 2 d A = ∫ 1 2 x 2 2 y 2 x = - 2 x = 2 d y

∬ R 1   x y 2 d A = ∫ 1 2 y 2 2 - 2 d y

∬ R 1   x y 2 d A = 0

Passo 5

Calcular a integral de R 2 :

∬ R 2   x y 2 d A = ∫ 0 1 ∫ - 2 - 1 x y 2 d x d y

∬ R 2   x y 2 d A = ∫ 0 1 x 2 2 y 2 x = - 2 x = - 1 d y

∬ R 2   x y 2 d A = ∫ 0 1 y 2 1 2 - 2 d y

∬ R 2   x y 2 d A = - 3 2 ∫ 0 1 y 2 d y

∬ R 2   x y 2 d A =   - 3 2 ( y 3 3 0 1 )

∬ R 2   x y 2 d A =   - 1 2

Passo 6

Calcular a integral de R 3 :

∬ R 3   x y 2 d A = ∫ 0 1 ∫ 1 2 x y 2 d x d y

∬ R 3   x y 2 d A = ∫ 0 1 x 2 2 y 2 x = 1 x = 2 d y

∬ R 3   x y 2 d A = ∫ 0 1 y 2 2 - 1 2 d y

∬ R 3   x y 2 d A = 3 2 ∫ 0 1 y 2 d y

∬ R 3   x y 2 d A = 3 2 ( y 3 3 0 1 )

∬ R 2   x y 2 d A =   1 2

Passo 7

Somar os resultados encontrados

∬ R   x y 2 d A = ∫ 1 2 ∫ - 2 2 x y 2 d x d y + ∫ 0 1 ∫ - 2 - 1 x y 2 d x d y + ∫ 0 1 ∫ 1 2 x y 2 d x d y

∬ R   x y 2 d A = 0 - 1 2 + 1 2

∬ R   x y 2 d A = 0

Resposta

0

Exercício Resolvido #4

Howard Anton, Irl Bivens, Stephen Davis, Cálculo – Volume II, 8ª ed. Porto Alegre: ARTMED EDITORA S.A, 2005, pág 1035-59.

Se

f x , y = 10.000 e y 1 + x 2

representa a “densidade populacional” de certo tipo de bactéria no plano x y , onde x e y são medidos em centímetros, encontre a população total de bactérias dentro do retângulo - 5 ≤ x ≤ 5 e - 2 ≤ y ≤ 0 .

Passo 1

Vamos pensar: se f ( x , y ) é a densidade populacional em termos de área, f representa quantas bactéricas existem por centímetro quadrado em cada ponto ( x , y ) . Então, para encontrar a quantidade de bactérias existente em uma área, precisamos integrar a função densidade nessa região, certo? Isso porque densidade vezes área é igual à quantidade de bactérias.

Temos o seguinte:

P = ∬ R   f ( x , y ) d A = ∬ R   10.000 e y 1 + x 2 d A

Onde R é o retângulo - 5 ≤ x ≤ 5 e - 2 ≤ y ≤ 0 .

Passo 2

Vamos desmembrar a integral utilizando o Teorema de Fubini.

∬ R   10.000 e y 1 + x 2   d A = ∫ - 5 5 ∫ - 2 0 10.000 e y 1 + x 2 d y   d x

Note que o intervalo da integral de fora está de acordo com d x e o da de dentro, com d y . E se você quisesse integrar ao contrário? Sem problemas, basta o intervalo estar de acordo.

Passo 3

Agora você deve integrar em relação a y ,   ou seja, resolver a integral de dentro (tomando x como constante).

= ∫ - 5 5 ∫ - 2 0 10.000 e y 1 + x 2   d y d x

Como x é constante, podemos tirar 10000 1 + x 2 da integral de dentro, ficando assim

= ∫ - 5 5 10.000 1 + x 2 ∫ - 2 0 e y d y d x

= ∫ - 5 5 10.000 1 + x 2 e y y = - 2 y = 0 d x

Substituindo os limites de integração de y ,

= ∫ - 5 5 10.000 1 + x 2 e 0 ⏟ 1 - e - 2 d x

∫ - 5 5 10.000 1 + x 2 ( 1 - e - 2 ) d x

Resolvida a integral de dentro, seguimos para a segunda integral!

Passo 4

Resolvida a integral de dentro, seguimos para a segunda integral!

Devemos, então, integrar em relação a x :

∫ - 5 5 10.000 1 + x 2 ( 1 - e - 2 ) d x

Tirando as constantes da integral

= 10.000 1 - e - 2 ∫ - 5 5 1 1 + x 2 d x =

Agora, para essa integral que restou, temos que nos lembrar do seguinte:

x = x ,         x ≥ 0 - x ,               x < 0

Perceba que os limites da integral são - 5 ≤ x ≤ 5 . Ou seja, temos parte que x ≥ 0 e parte que x < 0 , precisamos separar isso! Olha como fica

= 10.000 1 - e - 2 ∫ - 5 0 1 1 - x 2 d x + ∫ 0 5 1 1 + x 2 d x

O sinal ficou trocado porque na primeira integral temos x < 0 , enquanto na segunda temos x ≥ 0 .

Agora temos duas integrais em função de   x para resolver.

Passo 5

Vamos começar fazendo

∫ - 5 0 1 1 - x 2 d x

Vamos resolver primeiro sem os limites pra organizar melhor

∫ 1 1 - x 2 d x

Para resolver essa integral, vamos utilizar a técnica de substituição simples.

Aqui, vamos fazer a seguinte substituição,

1 - x 2 = u

Derivando u , fica assim

- d x 2 = d u → d x = - 2 d u

Assim, temos

∫ 1 1 - x 2 d x = ∫ 1 u - 2 d u = - 2 ∫ 1 u d u = - 2 ln ⁡ u

Lembrando que u = 1 - x 2 , temos

- 2 ln ⁡ 1 - x 2

Agora, olhando para os limites de integração,

∫ - 5 0 1 1 - x 2 d x = - 2 ln ⁡ 1 - x 2 x = - 5 x = 0 = - 2 ln ⁡ 1 ⏟ 0 + 2 ln ⁡ 1 - - 5 2 = 0 + 2 ln ⁡ 7 2

Passo 6

Agora, vamos ver a outra integral

∫ 0 5 1 1 + x 2 d x

Vamos resolver primeiro sem os limites pra organizar melhor

∫ 1 1 + x 2 d x

Novamente, vamos utilizar a mesma técnica de integração, substituindo assim,

1 + x 2 = u

Assim

d x 2 = d u → d x = 2 d u

Assim, temos

∫ 1 1 + x 2 d x = ∫ 1 u 2 d u = 2 ∫ 1 u d u = 2 ln ⁡ u

Voltando para x

2 ln ⁡ u = 2 ln ⁡ 1 + x 2

Agora, olhando para os limites de integração

∫ 0 5 1 1 + x 2 d x = 2 ln ⁡ 1 + x 2 x = 0 x = 5 = 2 ln ⁡ 1 + 5 2 - 2 ln ⁡ 1 ⏟ 0 = 2 ln ⁡ 7 2

Passo 7

Voltando para a integral que tínhamos no final do Passo 4,

= 10.000 1 - e - 2 ∫ - 5 0 1 1 - x 2 d x + ∫ 0 5 1 1 + x 2 d x

Vamos colocar o resultado

10.000 1 - e - 2 ∫ - 5 0 1 1 - x 2 d x + ∫ 0 5 1 1 + x 2 d x = 10.000 1 - e - 2 2 ln ⁡ 7 2 + 2 ln ⁡ 7 2 =

40.000 1 - e - 2 ln ⁡ 7 2

Resposta

∫ - 5 5 ∫ - 2 0 10.000 e y 1 + x 2 d y   d x = 40.000 1 - e - 2 ln ⁡ 7 2

Exercícios de Livros Relacionados

Calcular underset(R)(∬) f (x , y) d x d y , onde:b) f (x , y) = y e^(x y) ; R é o retângulo (0 = x = 3)/(0 = y = 1)
Calcule a integral dupla. ∬ R s e n ( x + y ) d A ,R = x , y 0 ≤ x ≤ π 2 ,0 ≤ y ≤ π 2
Calcule a integral iterada. ∫ - 3 3 ∫ 0 π / 2 ( y + y 2 c o s x ) d x d y
Calcule a integral iterada. ∫ 0 1 ∫ 0 3 e x + 3 y d x d y
Utilize um sistema de computação algébrica para determinar o valor exato da integral ∬ Rx 5 y 3 e x y d A onde R = 0 ,1 × 0 ,1 . Em seguida, use o SCA para desenhar o sólido cujo volume é dado pela in