Integrais Triplas em Regiões Cúbicas
Produzido por Arthur Melo de AlmeidaTeoria
Definição
Até aqui você já viu integrais simples (definidas para funções de uma variável) e integrais duplas (para funções de duas variáveis). Agora vamos expandir mais ainda esse conceito: vamos definir as integrais triplas para funções de três variáveis . E você achou que não dava pra piorar, né? Calma, não é tão complicado quanto parece : )
Enquanto para as integrais simples o intervalo de integração infinitesimal era (um comprimento) e para as duplas era (uma área), para as triplas teremos um volume infinitesimal , que pode ser representado assim:
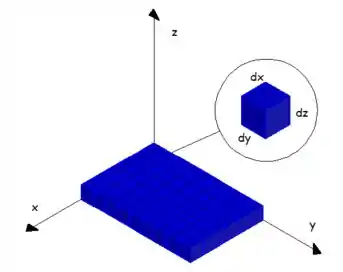
Sendo assim, a integral tripla de é definida dessa forma:
Esse termo dentro do limite é a Soma Tripla de Riemann, muito semelhante com o que vimos para as integrais simples e para as duplas. E assim como vimos para as duplas, o método prático de calcular integrais triplas é através de integrais iteradas. Temos, então, o Teorema de Fubini para integrais triplas:
Ou seja, vamos integrar por etapas, em relação a , e .
Da mesma forma que tínhamos mais de uma ordem de integração para as integrais duplas ( ou ), as triplas também podem ser escritas em mais de uma maneira. Na verdade, em seis maneiras! Você deve usar a que for mais conveniente para o exercício.
Mas, e ai, como calcular essas integrais? Seguindo o mesmo raciocínio que usamos para as integrais duplas, lembra como era?
Quando integramos em relação a uma variável, as outras serão tomadas como constantes. Lembre-se sempre que uma integral tripla, como uma dupla, sempre te dá um número, nunca uma função, ou seja, depois de integrar 3 vezes, se você não obteve um número, tem algo errado.
Vamos calcular a seguinte integral tripla:
Onde é o paralelepípedo dado por:
Passo 1: Sempre que a nossa região de integração for essa “caixa” limitada por números só, podemos usar qualquer uma das seis ordens de integração, vamos escolher . Como já temos os intervalos de cada variável, é só jogar isso ai na integral. Nesse caso, a integral iterada passa a ser:
Repare que varia de a , como escrevemos na integral de fora, varia de a , como está na integral do meio e varia de a , como na integral de dentro. Você tem que tomar muito cuidado para não confundir os intervalos!
Passo 2: Começaremos integrando em relação a (integral de dentro):
Passo 3: Agora vamos integrar em relação a :
Viu? É muito parecido com o que você fez até agora calculando integrais duplas!
Vamos ver alguns exercícios desse tipo pra fixar bem esse conceito, ele é muito importante para o entendimento do resto desse assunto!
Exercícios Resolvidos
Exercício Resolvido #1
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009
Calcule a integral:
Passo 1
Repare que nessa questão os limites de integração já estão posicionados na integral, é válido lembrar também que devemos resolver sempre de dentro para fora, ou seja, primeiro integraremos em depois em e por último em .
Quando vamos integrar em relação a , consideramos e constantes, lembra? Fica assim então, integrando em :
Passo 2
Vamos integrar em agora, certo? Temos que considerar constante então:
Passo 3
Integrando em temos:
Resposta
Exercício Resolvido #2
Elaboração Própria
Calcule a integral:
Passo 1
Vamos resolver a integral de dentro para fora, certo? Então vamos integrar primeiro , depois e finalmente . Vamos lá?
Para integrar , vamos considerar e como constantes, fica assim:
Passo 2
Para integrar em , vamos considerar como constante:
Muito cuidado nessa hora! Tem termos de e de , então substitua e com calma termo por termo!
Passo 3
Finalmente, integrando em :
Resposta
Exercício Resolvido #3
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009
Calcule a integral:
Passo 1
Integrando de dentro para fora, fazemos primeiro a integral em :
Obs: Note que quando você deriva , pela regra da cadeia, você ficaria com:
Portanto a integral de é simplesmente o seno da mesma função!
Voltando para a nossa integral:
Passo 2
Integrando em :
Passo 3
Finalmente, integrando em :
Só que sabemos que para qualquer
Logo:
Portanto: