Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 31
Determine o volume do sólido dado. O tetraedro sólido com vértices .
Passo 1
E aí meus queridxs, tudo bom com vocês? Vamos lá, precisamos calcular o volume do sólido descrito no problema, o que nada mais é do que calcular a integral acima de acordo com a região dada. Primeiramente, vamos observar como é nossa região de integração que é dada por
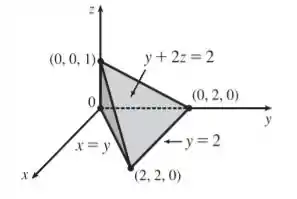
Agora, escreveremos nossa integral de forma iterada, para facilitar nossa resolução, de modo que obteremos
Passo 2
Agora que temos nossa integral de forma iterada, fica simples de resolver nosso problema pois basta vir resolvendo a integral da mais interna para a mais externa, sem nos esquecer, é claro, que ao integrarmos em uma variável devemos considerar a outra como constante. Sendo assim, resolvendo a integral mais interna temos
Dessa forma, ficamos com a seguinte integral dupla a ser resolvida
Continuando a resolução novamente com a integral mais interna vamos ter
Por fim, ficamos com a seguinte integral simples
Pronto, tá resolvido nosso exercício.