Assíntota Vertical e Horizontal
Produzido por Matheus dos Santos SoaresTeoria
Oiee! Seja bem vindo ao RespondeAí! Vem comigo pra a gente aprender TUDO o que você precisa saber sobre Assíntota Vertical e Horizontal!
Mas antes de qualquer coisa...
O que é uma assíntota?
Vamos dar uma olhada no gráfico da função
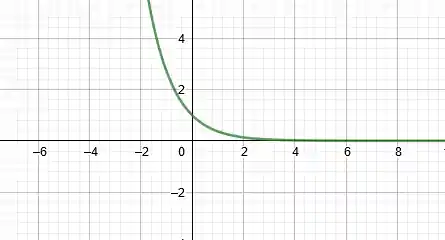
O que será que acontece se a gente colocar um valor de
Na realidade, o que acontece é que a nossa função fica muito perto de zero mas nunca chega a encostar no eixo
Ou seja, podemos dizer que uma assíntota horizontal ou vertical nada mais é do que uma reta imaginária que delimita a aproximação de uma função no gráfico à medida que ela cresce ou decresce.
Assíntota Vertical
No exemplo acima vimos uma assíntota horizontal, vamos dar uma olhada agora em assíntota vertical!
Se liga no gráfico da função
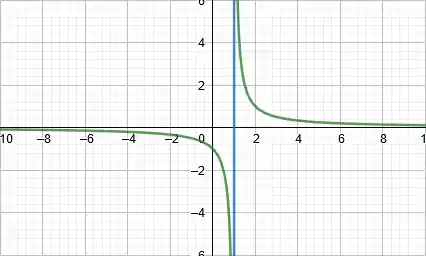
Se a gente olhar com calma a medida que o valor de
Logo, a reta
Mas a gente resolveu o problema apenas olhando pro gráfico, como faz pra resolver se não tivermos ele?
Então, perceberam que a gente basicamente viu que quando a função chegava muito perto de x=1 (pela direita e pela esquerda) ela explodia pra mais e pra menos infinito? Opa, então o que a gente fez foi basicamente resolver esses limites aqui, olha só:
Então basta resolvermos dois limites e eles resultarem em
Mas por que escolhemos o
No caso do nosso exemplo, a nossa função era:
Podemos ver que
Então, para achar as assíntotas verticais, vamos procurar valores de
Devemos ficar ligados principalmente em casos em que o denominador resulta em
Sendo assim, depois de achar esses valores que dão problema na função, a gente resolve o limite com tendendo pra eles tanto pela direita quanto pela esquerda:
Se um desses dois limites explodirem para mais ou para menos infinito. Isso é, o limite tendendo a
Você terá encontrado uma assíntota vertical naquele sentido 😉.
Assíntota horizontal
No exemplo inicial vimos que o eixo
O que a gente vai fazer agora é descobrir como achar a assíntota horizontal a partir da função!
Vamos pegar o exemplo inicial, já sabemos que a assíntota da função é
Podemos dizer que:
Maneiro! Chegamos que o nosso limite é igual a zero e o eixo x é justamente a reta
Então, quer dizer que para acharmos uma assíntota horizontal basta a gente resolver dois limites:
Onde
Se um ou os dois limites resultarem em um valor finito, ou seja, não explodirem pra mais ou menos infinito, quer dizer que encontramos uma assíntota horizontal. Vamos supor que um dos limites resultou em
Só fica atento que não é necessário que os dois limites sejam iguais a uma constante para ser uma assíntota, mas apenas um deles. Caso os dois limites resultem em constantes diferentes, teremos duas assíntotas, uma em cada constante.
Resumo
Passo a passo para achar a assíntota vertical
Para a gente achar possíveis assíntotas verticais nós temos que:
- Achar valores de que dão problema na nossa função, ou seja, que não estão no domínio dela (lembrar dos principais casos);
- Fazer os limites laterais da função com
tendendo aos valores problemáticos; - Se um desses limites laterais explodirem para mais ou menos infinito, quer dizer que temos uma assíntota vertical;
- Se os dois limites resultarem em constantes, não temos assíntotas verticais.
Passo a passo para achar a assíntota horizontal
E para acharmos assíntotas horizontais:
- Fazer os limites da nossa função com
tendendo a mais e menos infinito; - Se pelo menos um desses limites resultar em uma constante. Teremos que a reta é uma assíntota horizontal;
- Se os limites derem constantes diferentes, teremos duas assíntotas;
- Se os dois limites explodirem para mais ou pra menos infinito, não temos assíntotas horizontais.
Curtiu nosso conteúdo?!
Confere só esse vídeo sobre assíntota horizontal e vertical que eu separai especialmente pra você!
Vamos praticar com exercícios?
Assíntota Vertical
Assíntota horizontal
Resumo
Exercícios Resolvidos
Exercício Resolvido #1
UNICAMP - Cálculo 1 - P1 2015 Noturno – 3
Encontre as assíntotas verticais e horizontais da seguinte função
Passo 1
Antes de qualquer coisa vou analisar os dois termos (numerador e denominador) de e tentar abrir em um produto de polinômios irredutíveis.
Podemos simplificar , dessa forma:
Mesmo cortando o em cima e embaixo, está fora do domínio, por zerar o denominador original.
Ok, vamos procurar as assíntotas agora.
Passo 2
Seguinte, Assíntotas verticais aparecem onde o domínio não está definido e as horizontais aparecem quando usamos o limite em .
Começando com as verticais, o domínio não está definido em
Assíntota vertical em .
OBS: Repara que também não está no domínio da função original, já que aparece um no denominador de . Porém, o que acontece é que, ao calcularmos seu limite quando veremos que ele converge para um valor, e não para , não consistindo em uma assíntota vertical!
Passo 3
Vamos usar o limite de em e em
Achamos uma mesma assíntota horizontal, .
Resposta
Exercício Resolvido #2
PUC-RJ - Cálculo B - P2 2014.2 - 3 a b
Seja . Determine o que se pede, justificando adequadamente o que não há.
Domínio de .
Assíntotas horizontais e verticais da curva
Passo 1
Para o domínio de devemos lembrar que o termo dentro de um logaritmo deve sempre ser maior , enquanto o termo dentro de uma raiz quadrada deve sempre ser maior ou igual a.
Vamos analisar dentro da raiz. Lá temos a seguinte condição,
Repara que temos do somatório de e são valores sempre positivos. Ou seja, não teremos nenhuma restrição para raiz.
Seguindo o mesmo raciocínio para analisar a parte logarítmica, temos que o resultado da raiz sempre será positivo. Não havendo restrições também.
Portanto, temos que,
Passo 2
Uma vez que não existem descontinuidades no domínio não teremos assíntotas verticais.
Vamos focar nas assíntotas horizontais. Podemos pensar na assíntota como uma linha horizontal imaginaria que nunca será tocada.
Para isso, verificamos o limite em
Primeiro vamos de
Repara que ele vai para o infinito, então não temos uma linha na horizontal que não será cortada, já que a função tá sempre subindo.
Agora vamos analisar
Aqui encontramos uma assíntota horizontal em .
A gente já encontrou a assíntota, mas vamos olhar o gráfico por curiosidade,
Repara que temos uma linha horizontal imaginaria quando vamos para valores de negativos.
Resposta
Exercício Resolvido #3
CEFET - Cálculo 1 - P1 Romulo 2014.2 – 4
Encontre as assíntotas horizontais e verticais:
Passo 1
Vamos escrever em forma de primeiro:
Que fique claro, é bom analisar logo o domínio dessa função. Seu denominador não pode zerar, o que acontece em e em . Seu domínio será, portanto:
Passo 2
Para ver assíntotas horizontais lançamos o limite para da função:
Agora para :
Pelos resultados temos duas assíntotas horizontais de mesma equação, .
Passo 3
Para assíntotas verticais temos que olhar para onde o domínio da função não está definido (nesse caso, em ) e lançar os limites laterais ali:
Feito isso, sabemos que temos assíntotas verticais em e
Resposta
Exercício Resolvido #4
UFF - Cálculo IA - P1 Humberto 2014.1 – 2 e
Determine, caso existam, as assíntotas horizontais e verticais do gráfico da função abaixo
Passo 1
Vamos olhar para a e seu domínio, em primeiro lugar. Quando ela vale , mas para , ela vale a seguinte função:
Bom, o domínio desse cara aqui de cima, para não zerar o denominador, é . Com isso, a gente conclui que ele está definido exclusivamente numa região em que ele existe, sem descontinuidades! Não teremos assíntotas verticais, portanto, em .
Passo 2
Agora, em nós precisamos calcular os limites laterais, pois temos uma descontinuidade!
Repara, ambos se resolvem pelo limite fundamental, já que:
Enfim, a conclusão é que, por mais que os limites laterais (que valem ) não batam com o valor de no ponto (que é ), eles não explodem para , não gerando assíntotas verticais.
Passo 3
Caçamos as assíntotas horizontais jogando os limites para . Começamos fazendo o :
O jeito de resolver esse cara é usar o Teorema do Confronto:
Pelo mesmo raciocínio, encontraremos:
Achamos a mesma assíntota horizontal para os dois lados, .
Resposta
Exercício Resolvido #5
Elaboração própria
Determine, caso existam, as assíntotas horizontais e verticais do gráfico da função abaixo
Passo 1
Vamos olhar para a e seu domínio, em primeiro lugar. Quando , vemos que a função da problema porque:
Bom, o domínio desse cara aqui de cima, para não zerar o denominador, é . Como é um ponto que gera indeterminação, esse ponto é um candidato pra assíntota vertical
Passo 2
Agora, em nós precisamos calcular os limites laterais, pois temos uma descontinuidade!
Repara, para ambos precisamos primeiro reescrever o limite. O denominador mais complicado é um polinômio de segundo grau que já sabemos uma das raízes, o próprio . A outra vai ser , tal que:
Se
Então
E logo:
Fazendo isso no limite:
Observando-o lateralmente temos:
E com isso, concluímos que é uma assíntota vertical!
Passo 3
Mas calma lá, o polinômio não tinha duas raízes? O que vai acontecer em ? Vamos substituir e ver:
Opa, outra indeterminação! Já que é assim, também é um candidato à assíntota vertical. Partiu então calcular o limite:
Observando-o lateralmente temos:
E com isso, concluímos que também é uma assíntota vertical!
Passo 4
E pra fechar com chave de ouro, falta só a gente checar as assíntotas horizontais. Para isso, precisamos fazer:
Como já vimos, esse limite vai ser igual à
Abrindo o denominador, temos:
Colocando os termos de maior ordem em evidência, ficamos com:
E, por fim, aplicando o limite:
E prontinho! Questão resolvida, agora é só partir pro abraço. Vamos ter que é também uma assíntota, só que esta é horizontal