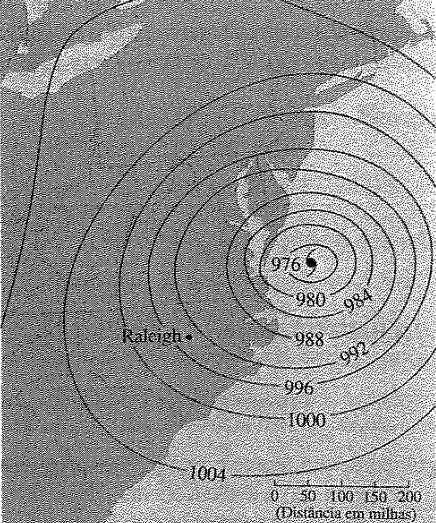
14.1. É dado o mapa de contornos mostrando a pressão barométrica (em milímetros) às 7:00 horas da manhã do dia 12 de setembro de 1960, quando o Furacão Donna estava ativo. Estime o valor da função pressão em Raleigh, na Carolina do Norte, em direção ao olho do furacão. Quais são as unidades da derivada direcional?
Passo 1
Queremos encontrar o valor da função pressão em Raleigh. Uma forma de fazer isso é imaginar uma linha que passar por Raleigh e pelo olho do furacão.
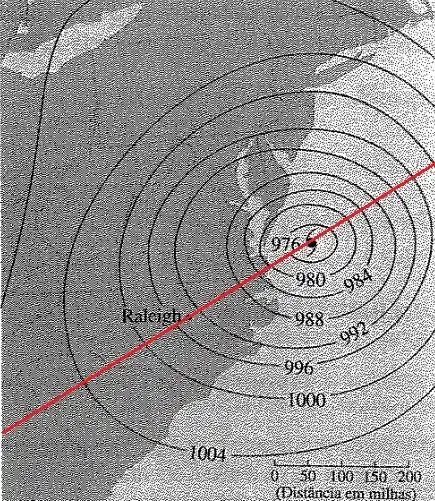
Passo 2
Agora podemos usar essa linha para ver o como a pressão vai mudado em relação ao olho do furacão. Repare que pelos dados que temos, um ponto próximo de Raleigh, tem uma pressão de 996 milibars, enquanto outro ponto próximo a Raleigh, só que mais perto do olho do furacão, tem uma pressão de 992 milibars. Em outras palavras, quando estamos indo na direção do olho do furacão pela linha que traçamos a pressão muda de 996 milibar para 992 milibars. E usando a escala da imagem podemos aproximar a distância entre essas duas marcações para 40 milhas.
Passo 3
Com essas informações podemos concluir que a função pressão é
E sua unidade é