Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.2 - Ex. 6
15.6. Calcule a integral iterada.
Passo 1
Faaaaaala turminha, tudo bem? Vamos começar!
O enunciado pede para calcular a integral iterada e fornece a seguinte integral dupla:
Tá, mas o que é integral iterada? E como faz isso?
Vamos com calma. A integral iterada nada mais é que uma integral que tem mais de uma variável, e podemos deixar ela escrita igual a forma abaixo. Assim, começamos a integrar de dentro para fora.
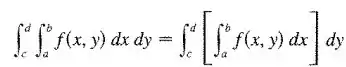
Vamos deixar nossa integral nesse formato, e começamos a integrar em , aplicamos os limites de integração e repetimos o processo para .
Show pessoal! Vamos lá colocar mão na massa!
Passo 2
Vamos lá, temos que resolver a seguinte integral dupla:
Lembra que falamos antes, vamos deixar a integral com a cara de uma integral iterada, vai ficar assim:
A gente tem que integrar primeiro em e depois em .
Passo 3
Começando a integrar por dx.
Para facilitar, vamos lembrar que a integral da soma é a soma das integrais, então
Agora está mais fácil de resolver né! Vamos integrar:
Aplicando os limites de integração, vamos ter:
Passo 4
Agora ficamos com uma integral simples em .
De novo temos uma soma dentro da integral, logo podemos separar novamente:
Integrando, vamos ter:
Aplicando os limites de integração, temos:
Resolvendo vamos ter:
Ou seja,