Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.5 - Ex. 43
Um lado de um triângulo está aumentando em uma taxa de e um segundo lado está decrescendo em uma taxa de . Se a área do triângulo permanece constante, a que taxa varia o ângulo entre os lados quando o primeiro lado tem de comprimento, o segundo lado tem de comprimento e o ângulo é ?
Passo 1
Oie, tubo bem? Vou te ajudar a entender e resolver essa atividade.
A gente tem uma situação onde um lado de um triangulo aumenta em uma taxa:
E um outro lado diminui em outra taxa:
Porém a área do triangulo permanece a mesma, sendo assim, algo precisa também variar para que a área permaneça a mesma. Aqui eles nos pedem a taxa de variação do ângulo no momento especifico:
Então pessoal, antes de resolvermos o problema vamos desenhar o triângulo para facilitar nossa visualização:
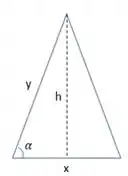
Da geometria sabemos que a área de um triângulo é dada por:
Para essa situação:
Agora temos que encontrar a derivada de em relação a , ou seja, , pois a derivada significa taxa de variação, que é o que precisamos.
Passo 2
Para a nossa situação sabemos que a área é dada por:
Mas quem seria esse ? Utilizando trigonometria conseguimos tirar que:
Substituindo na expressão da área, teremos:
O enunciado nos informa que a área não varia com o tempo, sendo assim podemos dizer que:
Isso é, a taxa de variação da área é nula.
Mas quem seria essa derivada? Utilizando a regra da cadeia teremos o seguinte:
O problema nos pede a taxa que varia o ângulo, ou seja, a gente quer descobrir
Fazendo as derivadas, temos:
Agora derivando em relação a :
E agora por ultimo em relação a :
Substituindo, teremos:
Isolando :
Passo 3
Tudo bem, agora chegamos em uma expressão interessante para resolver nosso problema! Segundo o enunciado temos que:
A taxa de variação de um lado é:
E a do outro é:
Substituindo esses valores, teremos:
Temos então: