Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 7.8 - Ex. 2

2)Calcular ∬_R^() sen (x^2 + y^2) d x d y onde R é a região da Figura 7.33.

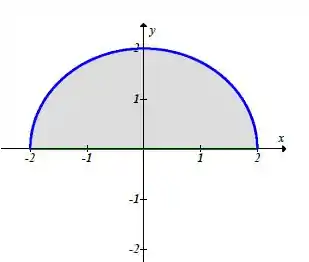
Passo 1

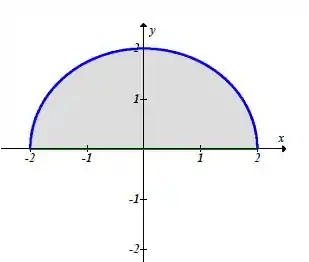
Ao analisar o gráfico, temos:

- 2 <= r <= 2

0 <= theta <= pi

Pelas coordenadas polares, temos que:

x = r * cos theta

y = r * sen theta

J a c o b i a n o = r

Dessa forma, temos:

x^2 + y^2 = r^2 * cos^2 theta + r^2 * sen^2 theta

cos^2 + sen^2 = 1

Logo,

= r^2 * cos^2 theta + r^2 * sen^2 theta = r^2

Dessa forma, temos:

∬_(0 0)^(pi 2) ( sen r^2 ) r d r d theta

Passo 2

Primeiro vamos integrar com relação a r ,

int_0^2 ( sen r^2 ) r d r =

Nesse caso, vamos resolver pelo método da substituição. Vamos chamar,

u = r^2

d u = 2 r :. r = (d u)/(2)

Dessa forma:

(1)/(2) int sen u d u

= (1)/(2) * (- cos u) + c

Voltando com u = r^2

((1)/(2) (- cos r^2)|_0^2 =

(1)/(2) * ( - cos 4 + 1 )

Passo 3

Agora vamos integrar em relação a theta ,

int_0^(pi) - (1)/(2) cos 4 + (1)/(2) d theta =

((1)/(2) - (1)/(2) cos 4|_0^(pi) = (- (1)/(2) cos 4 + (1)/(2)) pi

Resposta

(- (1)/(2) cos 4 + (1)/(2)) pi

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 2 ∫ 0 4 - x 2e - x 2 - y 2 d y d x
Calcule a integral iterada convertendo para coordenadas polares. ∫ 0 1 / 2 ∫ 3 y 1 - y 2x y 2 d x d y
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∫ R ∫ f x , y d A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .3.
Uma região é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∬ R f x ,yd A como uma integral iterada, onde f é uma arbitrária qualquer contínua em R .
29- Calcule a integral iterada, convertendo-a antes para coordenadas polares: ∫ 0 1 ∫ 0 1 - x 2 e x 2 + y 2 d y d x