Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 40
38. Para as funções de uma variável, é impossível uma função continua ter dois pontos de máximo local e nenhum ponto de mínimo local. Para funções de duas variáveis, esse caso existe. Mostre que a função
Só tem dois pontos críticos, ambos de máximo local. Em seguida, utilize um computador para desenhar o gráfico com uma escolha cuidadosa de domínio e de ponto de vista para ver como isso é possível.
Passo 1
Oie, tudo bem? Vamos resolver essa atividade.
Dada a função:
Queremos mostrar que por essa função ser de duas variáveis, podemos ter pontos de críticos de máximo local.
Então precisamos provar que a função só tem dois pontos críticos, a ambos são pontos de máximo.
Já temos nossos pontos de interesse, mas falta dizer se são máximos, mínimos ou pontos de sela, para isso a gente precisa da segunda derivada, vamos usar
Podem ocorrer três casos:
- então é um mínimo local.
- então é um máximo local.
- então não é nem mínimo e nem máximo local.
Então iremos provar aqui a letra b).
Passo 2
A função que ele nos deu foi a seguinte:
Para acharmos os pontos críticos, vamos fazer e . Então, vamos lá!
Derivando em relação a :
Logo,
Agora em relação a :
Assim,
Agora que já achamos e podemos igualar a . Beleza? Então vamos lá.
Para o :
E para o :
Passo 3
Da primeira equação, temos o seguinte:
Então temos o seguinte:
Substituindo na segunda:
Assim,
Logo,
ou
Portanto,
ou
Agora vamos ver se esses pontos realmente satisfazem.
Substituindo na primeira equação:
Então,
Opa! essa já deu ruim, pois nenhum atende a essa condição. Agora vamos ver para :
Na primeira:
Na segunda:
Dessa forma,
Isso quer dizer que só teremos um ponto crítico na nossa função, e ele será o seguinte:
Agora vamos aplicar o teste da segunda derivada para analisar os pontos críticos.
Passo 4
Vamos encontrar as derivadas parciais de segunda ordem para achar para usar na equação .
Usando do Passo :
Logo,
Para o :
Usando do Passo :
Logo,
Por fim, vamos ver como fica o :
Usando o que achamos no Passo :
Assim,
Passo 5
Para o ponto :
Para o :
Logo,
Para o :
Fazendo as contas:
Por fim, para :
Substituindo tudo em :
Portanto,
Como e , temos um ponto de máximo local.
Passo 6
Fazendo um gráfico com o auxilio do GeoGebra, temos:
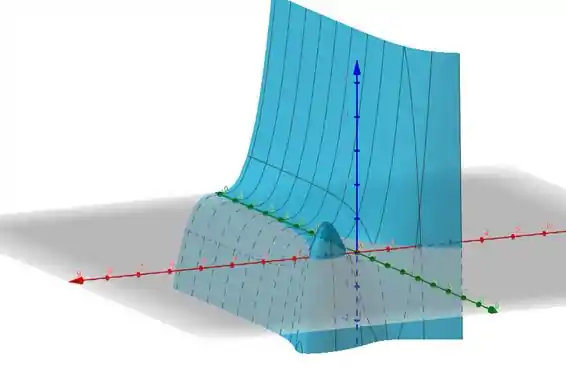
Como é possível verificar os dois pontos de máximo. 😉
Resposta
Como e , temos um ponto de máximo local.