Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 20
5-20. Determine os valores máximos e mínimos locais e pontos de sela da função. Se você tiver um programa de computador para desenhar em três dimensões, trace o gráfico da função usando um ponto de vista e domínio convenientes para mostrar os aspectos importantes da função.
20.
Passo 1
E aí, galerinha!
Neste exercício, temos a função:
Queremos saber quais são os pontos onde essa função tem valores máximos e mínimos locais. Também queremos saber se ela tem pontos de sela, que são aqueles onde a função muda de concavidade.
Para visualizar melhor a forma dessa função, podemos usar um programa de computador que faça o gráfico dela em três dimensões, escolhendo um intervalo adequado para e .
Mas como vamos resolver isso?
Para resolver esse problema, vamos seguir os seguintes passos:
- Calcular as derivadas parciais da função em relação a e , que nos dão a taxa de variação da função em cada direção.
- Igualar as derivadas parciais a zero e resolver o sistema de equações resultante, que nos dá os pontos críticos da função, onde ela pode ter máximos, mínimos ou pontos de sela.
- Aplicar o teste da derivada segunda, que nos permite classificar os pontos críticos de acordo com o sinal do determinante de uma matriz chamada hessiana, que contém as segundas derivadas da função.
- Identificar os valores máximos e mínimos locais e os pontos de sela da função, e verificar se eles estão dentro do domínio dado.
- Usar um programa de computador para fazer o gráfico da função e observar o seu comportamento.
Se e , o ponto é de mínimo, se o ponto é de máximo.
Se o ponto é de sela e se não podemos concluir nada.
Bora começar!
Passo 2
Para começarmos a análise dos máximos e mínimos da função, vamos primeiramente encontrar as derivadas parciais da mesma, se liga:
Pelas regras das derivadas trigonométricas:
Encontrando as derivadas de segunda ordem, teremos:
Para
Temos que ou , certo? Para , temos que ou .
Além disso, para , temos que .
Se substituirmos em teremos:
Para que isso seja zero, então ou .
Além disso, substituindo em teremos:
Para que isso seja zero, então .
Tranquilo até aqui?
Passo 3
Tudo bem, agora que fizemos a análise dos pontos em que a derivada é zero, podemos concluir que os pontos críticos são:
Agora o que temos que fazer é testar esses pontos em , que é dado da seguinte forma:
Mas quem é ? Como já calculamos , então será:
Se testarmos os pontos críticos em , teremos:
O resultado implica em ponto de sela como vimos no passo 1.
Como nesses casos , temos que anaisar ...
O resultado implica em pontos de máximos locais.
O resultado implica em pontos de mínimos locais.
Resumindo o que calculamos nesse passo temos:
Pontos críticos:
Pontos de sela:
Pontos de mínimos locais:
Pontos de máximos locais:
Show?
Passo 4
Agora vamos plotar o gráfico de
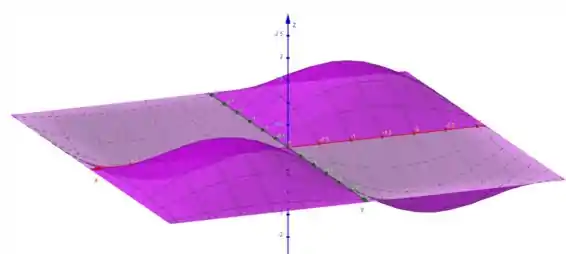
É isso! O que achou? Responde Aí!
Resposta
Pontos críticos:
Pontos de sela:
Pontos de mínimos locais:
Pontos de máximos locais: