Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.4 - Ex. 8
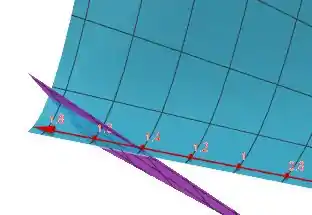
7-8. Desenhe a superfície e o plano tangente no ponto dado. (Escolhe o domínio e o ponto de vista de modo a ver tanto a superfície quanto o plano tangente.) Em seguida, dê zoom até que a superfície e o plano tangente se tornem indistinguíveis.
8.
Passo 1
Para determinarmos uma equação do plano tangente à superfície em um ponto específico devemos, assim como discutido na seção 14.4 do Stewart, determinar:
No qual os valores com subíndice se tratam do ponto dado pelo enunciado. Sendo assim, primeiramente vamos determinar as derivadas parciais no ponto dado:
Passo 2
Agora que já determinamos as derivadas parciais no ponto especificado, basta substituirmos , e , saca só:
Que é a equação do plano tangente que procurávamos! Plotando o gráfico contendo as duas curvas, teremos:
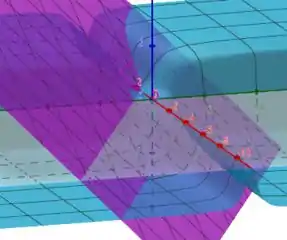
Onde o plano tangente se encontra em roxo e a superfície se encontra em azul claro. Se dermos zoom:
