Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 18
Uma agência de turismo está organizando um serviço de barcas, de uma ilha situada a de uma costa quase reta, para uma cidade que dista , como mostra a figura a seguir. Se a barca tem uma velocidade de por hora e os carros tem uma velocidade média de , onde deverá estar situada a estação das barcas a fim de tornar a viagem a mais rápida possível?
Passo 1
Incialmente, podemos fazer uma ilustração do que está acontecendo. Supondo uma distância até a estação das barcas, temos:
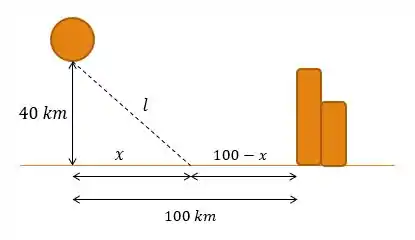
Para encontrarmos , podemos aplicar o Teorema de Pitágoras. Assim,
Então,
Logo, o tempo total ficará o seguinte:
Substituindo os dados:
Passo 2
Como queremos a viagem mais rápida, a ideia é minimizar o tempo. Para isso, vamos derivar a equação de e igualar a zero para encontrar os pontos críticos.
Derivando:
Cuidado para não esquecer da regra da cadeia!
Simplificando e igualando a zero:
Portanto,
Elevando ao quadrado dos dois lados:
Organizado as coisas:
Fazendo as contas:
Isto é,
Com isso, concluímos que a estação das barcas deve se localizar a uma distância de da cidade.
Resposta
A estação das barcas deve se localizar a uma distância de da cidade.