Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 5.12 - Ex. 13
Um cone reto é cortado por um plano paralelo à sua base. A que distancia da base deve ser feito esse corte, para que o cone reto de base na seção determinada, e de vértice no centro da base do cone dado tenha volume máximo?
Passo 1
Inicialmente, vamos supor que essa distância é e fazer um esboço do que está acontecendo, olha só:
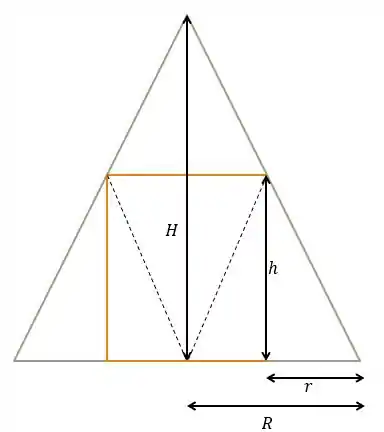
O cone que deve ter altura máxima é esse no meio do triângulo grande, sacou?!
Repare que o triangulo retângulo pequeno, é semelhante ao triangulo retângulo grande. Assim,
Logo,
Passo 2
Para acharmos o maior cilindro, vamos expressar o volume e maximizar. Vem comigo!
Logo,
Substituindo a expressão de que encontramos no Passo 1:
Assim,
Para maximizar, vamos derivar a expressão de e igualar a zero. Usando a regra do produto:
Igualando a zero:
Portanto,
Como :
Passo 3
Agora que já achamos a relação entre os raios, vamos usar a relação do Passo 1 para saber a altura .
Como :
Com isso podemos ver que o plano deve cortar o cone a um terço da altura em relação a base.
Resposta
A um terço da altura em relação a base.