Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.6 - Ex. 23
A Cia. Ltda. produz um determinado produto e vende-o com um lucro total dado por , onde representa a quantidade produzida. Determine o lucro máximo e a produção que maximiza o lucro. Esboce o gráfico desta função.
Passo 1
Vamos derivar a função lucro e igualar a zero, a fim de achar os possíveis pontos de máximo:
Passo 2
Como , o lucro máximo só pode ser obtido com ou :
Assim, o lucro máximo é e a produção que maximiza o lucro é .
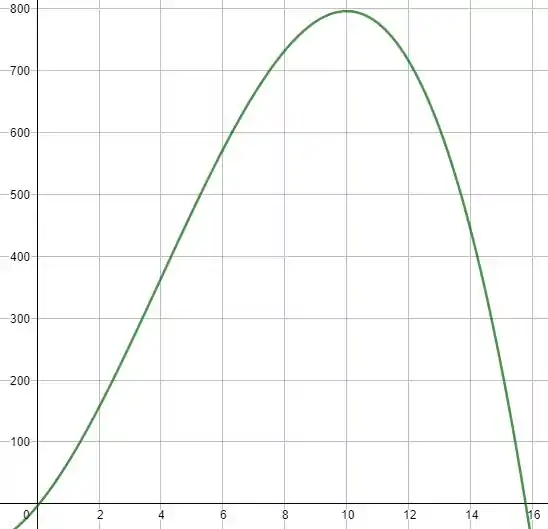
Um esboço do gráfico da função é feito a seguir, para ilustrar isso:
Resposta
Exercícios de Livros Relacionados
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. g
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. g
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. h
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. G
Ache os extremos absolutos da função dada no intervalo indicado, se existirem, e determine os valores de x nos quais ocorrem os extremos absolutos. Faça um esboço do gráfico da função no intervalo. F