Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 14.3 - Ex. 4
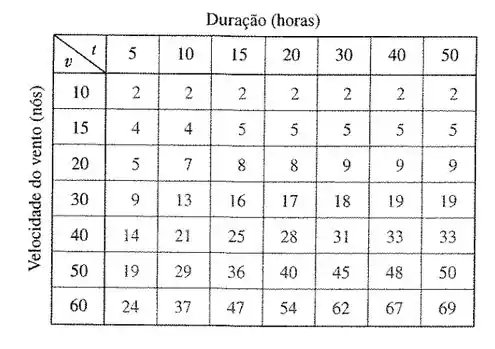
A altura das ondas em mar aberto depende da velocidade do vento e do tempo durante o qual o vento se manteve naquela intensidade. Os valores da função são apresentados em pés na tabela.
Qual o significado das derivadas parciais e ?
Estime os valores de e . Quais são as interpretações práticas desses valores?
Qual parece ser o valor do seguinte limite?
Passo 1
Fala ai pessoal. Tranquilo?
Bora fazer uma questãozinha!
A questão será dividida em três partes.
- Na letra A temos que dizer o que e significam em termos de qualquer função.
- Na letra B, teremos que usar a definição de derivadas parciais.
- Na letra C, pede para encontrarmos o valor do limite quando o tempo tende ao infinito. Para isso, a melhor forma de resolver é analisando a tabela, como a função se comporta quando a velocidade se mantém e a variável é o tempo? Fica a dica!
Observação importante!!! Na tabela nos dá a variação da temperatura e unidade, isso significa que teremos que escolher dois pontos (antes e depois do ponto dado) para calcular e no final verificar a média pela equação.
É isso pessoal, agora �� só resolver!
Passo 2
a) Derivada parcial
- Representa a taxa de variação da altura das ondas em relação com a velocidade do vento.
- É a taxa de variação instantânea de com relação aa , mantendo todas as outras variáveis constantes.
Agora a derivada parcial
- Representa a taxa de variação da altura das ondas em relação com a variação do tempo.
- Duas variáveis precisam estar correlacionadas e qualquer outra variável do problema precisa estar constante.
Passo 3
b) Os valores de pela tabela representam os valores da taxa de variação da velocidade em relação com o tempo e representa o valor da taxa de variação do tempo em relação com a velocidade e podemos encontrar de acordo com a definição da derivada abaixo:
Precisamos encontrar a taxa de variação instantânea da velocidade e para isso vamos fazer a média aritmética da variação após com a variação anterior ao ponto dado.
A média aritmética só é válida pois os pontos em v e em t são igualmente espaçados.
Passo 4
Considerando a função , em que a variação anterior é e a depois é , substituindo.
Observando na tabela, temos que:
Substituindo os valores dados no enunciado podemos calcular e .
A taxa de variação instantânea, será
Passo 5
Vamos usar os mesmos procedimentos para calcular .
A variação agora está em termos do tempo. Perceba que a tabela, a coluna varia de em . Logo
Substituindo os valores dados no enunciado podemos calcular e .
Agora :
A taxa de variação instantânea, será
O valor de significa que no instante onde a velocidade em nós é de 40 nós e a duração é de horas temos uma variação da altura das ondas no tempo de 1 pé por hora e representa a variação da altura da onda por nó, pés por nó.
Passo 6
c) O valor de é dado por:
Onde é uma função das variáveis e . Fixando uma velocidade e analisando somente os tempos nós notamos que à medida que o tempo aumenta a duração h tende a permanecer a mesma, vamos analisar a velocidade de . Você vê que não faz diferença na altura para e . E isso independe para qualquer velocidade, no tempo infinito a altura para de variar, logo: