Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 20

  1. Aproxime f por um polinômio de Taylor com grau n em a .
  2. Use a desigualdade de Taylor para estimar a precisão da aproximação f x ≈ T n ( x ) quando x estiver no intervalo dado.
  3. Verifique seu resultado na parte (b) traçando R n x

20.

f x = x ln ⁡ x ,                     a = 1 ,                     n = 3 ,                     0,5 ≤ x ≤ 1,5

Passo 1

Fala, gente! Tudo belezinha?

Olha só, a questão nos deu uma função f x = x ln ⁡ x   e quer, no item (a), uma aproximação dela por um polinômio de Taylor, com a = 1 e n = 3 (iremos fazer três integrais, show?).

A partir disso, no item (b) pedem pra gente usar uma desigualdade de Taylor e estimar a precisão da aproximação da função f com o polinômio de Taylor no intervalo 0,5 ≤ x ≤ 1 , 5 .

E no item (c), verificar o resultado de (b), traçando R n x , que é básicamente f x - T n ( x ) .

Bora passo a passo entender e fazer essa questão.

Passo 2

  1. Primeiramente, para encontrar os polinômios de Taylor vamos usar o formato da série de Taylor é

    2. ∑ n = 0 ∞ f n ( a ) n ! x - a n

    Para n = 3 precisaremos até a terceira derivada, então derivando e substituindo no centro x = 1

    f = x ln ⁡ x ⇒ f 1 = 0

    f ' = ln ⁡ x + 1 ⇒ f ' 1 = 1

    f ' ' = 1 x ⇒ f ' ' 1 = 1

    f ' ' ' x = - 1 x 2 ⇒ f ' ' ' 1 = - 1

    Então nosso polinômio é

    T 3 = 0 + x - 1 + 1 2 ! x - 1 2 - 1 3 ! x - 1 3

    T 3 = x - 1 + 1 2 x - 1 2 - 1 6 x - 1 3

    Passo 2

  2. Para usar a desigualdade de Taylor temos a seguinte relação, se f n + 1 ( x ) ≤ M , então

    3. R n x < M n + 1 ! x - a n + 1

    Então para estimar o erro, vamos precisar primeiramente da quarta derivada

    f ' ' ' ' x = 2 x 3

    Agora precisamos de um valor M que seja maior que essa função em todo o intervalo 0,5 ≤ x ≤ 1,5 , para isso podemos analisar o seguinte, em todo o intervalo a função de f ' ' ' ' x está decrescente, então para pegarmos o maior valor da função, precisamos do menor valor do intervalo ( 0,5 ) e substituirmos, podemos dizer que

    f ' ' ' ' x ≤ f ' ' ' ' 0,5 ,                     0,5 ≤ x ≤ 1,5

    Então podemos usar

    M = f ' ' ' ' 0,5 = 2 ( 0,5 ) 3 = 16

    Passo 3

    Temos então que

    R 3 x ≤ 16 4 ! x - 1 4

    Agora precisamos do valor de x - 1 4 , no intervalo 0,5 ≤ x ≤ 1,5 , se subtrairmos 1 em todas as partes da inequação, ficamos com

    - 0,5 ≤ x - 1 ≤ 0,5

    Podemos colocar em módulo

    x ≤ 0,5

    Elevando a quarta potencia

    x 4 ≤ 0,0625

    Logo

    R 3 x ≤ 16 4 ! 0,0625

    R 3 x ≤ 0,04166 … = 4,2 × 10 - 2

    Passo 4

  3. Traçando o gráfico de | R n | , para achar a função R n vamos usar a definição que diz

R n = f x - T n

R 3 = x ln ⁡ x - T 3

R 3 = x ln ⁡ x - x - 1 + 1 2 x - 1 2 - 1 6 x - 1 3

R 3 = | x ln ⁡ x - x - 1 + 1 2 x - 1 2 - 1 6 x - 1 3 |

No plano

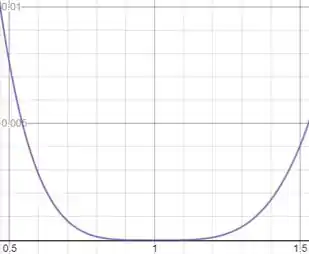
Resposta

  1. T 3 = x - 1 + 1 2 x - 1 2 - 1 6 x - 1 3

  2. R 3 x ≤ 4,2 × 10 - 2

  3. y = | R 3 ( x ) |

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use séries para aproximar a integral definida com a precisão indicada.60. ∫ 0 0,5 x 2 e - x 2 d x ,( e r r o0,001 )
Use multiplicação ou divisão de séries de potência para encontrar os três primeiros termos não nulos na série de Maclaurin para cada função. y = e x sen 2 ⁡ x
Mostre que se p for um polinômio de enésima ordem, então: p x + 1 = ∑ i = 0 n p i x i !
Use séries para aproximar a integral definida com a precisão indicada. ∫ 0 1 sen ⁡ x 4 d x ,( 4c a s a sd e c i m a i s )
Calcule a integral indefinida como uma série infinita. ∫ arctg ⁡ x 2 d x