Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.10 - Ex. 72
Use multiplicação ou divisão de séries de potência para encontrar os três primeiros termos não nulos na série de Maclaurin para cada função.
Passo 1
E aai galerinha, tudo bem? Vamos lá!!!
Usando de multiplicação ou divisão de series de potência, devemos encontrar os três primeiros termos não nulos na serie de Maclaurin para cada função.
Vish! Como faço essa?
Vamos olhar para a expressão dada. Você concorda que posso escrever ela desse jeito:
Agora vamos olhar para a tabela de séries de potências conhecidas, e ver se tem alguma que nos ajude.
Repare que temos uma série de potência para e para , isso é muito bom pessoal, pois agora só precisamos fazer a multiplicação dos termos.
Vamos começar!!! Essa vamos tirar de letra ein!!
Passo 2
Bom, vamos relembrar nossa função que queremos encontrar os três primeiros termos da série de potência:
Como vimos antes na , conhecemos as seguintes s��ries de potência:
Agora precisamos fazer a multiplicação entre as series.
Vamos fazer por partes, primeiro para:
Como queremos apenas os três primeiros termos, podemos pegar apenas os três primeiros termos de cada série. Logo, vamos ter:
Fazendo a multiplicação estilo chuveirinho:
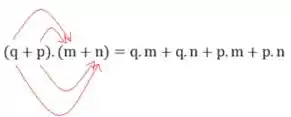
Vamos ter a seguinte resposta:
Simplificando, vamos ter:
Passo 3
Agora vamos precisar fazer a segunda parte da multiplicação, que é a resposta de:
Obtemos no passo anterior que:
E sabemos que:
Agora vamos fazer a multiplicação. Novamente vamos pegar apenas os três primeiros termos de cada expressão, pois já é suficiente para obter os três primeiros termos não nulos. Logo temos:
Fazendo a multiplicação chuveirinho, vamos ter:
Simplificando a função e escrevendo os termos com grau menor ou igual a , obtemos:
Sendo assim, simplificando a expressão e juntando os termos em comum, temos: