Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 14
(a) Aproxime por uma série polinomial de Taylor, com grau no ponto .
(b) Use a desigualdade de Taylor para estimar a precisão da aproximação quando está no intervalo dado.
(c) Verifique o resultado da parte anterior fazendo o gráfico de .
Passo 1
E aiiii minha turminha, tudo na paz com vocês?
Temos uma questão que solicita três itens.
No item (a) precisamos aproximar por uma série polinomial de Taylor, com grau no ponto . Já no item (b) usar a desigualdade de Taylor para estimar a precisão da aproximação quando está no intervalo dado. Por fim, no item (c) verificar o resultado da parte anterior fazendo o gráfico de .
Vamos pensar juntos em uma solução, beleza?
No item (a) vamos aplicar a série de Taylor conforme os dados fornecidos. A série Taylor é:
Vamos precisar encontrar o valor de cada (derivada aplicada no ponto ), e determinar a expressão . É interessante fazer uma tabela, para ficar organizado e de fácil compreensão.
Para o item (b), vamos aplicar a formula da desigualdade de Taylor:
Por fim, no item (c) precisamos fazer o gráfico de que foi encontrado no item (b).
Vamos começar então!!!
Passo 2
Item (a)
Nesse exercício iremos analisar a seguinte situação:
Sabemos que a série de Taylor tem essa cara:
A tabela a seguir mostra os valores para cada :
Lembrando que expandimos a serie até , para saber o comportamento na hora de aplicar a desigualdade de Taylor, se a série está decaindo.
Dessa forma, a série de Taylor para é dada por:
E, simplificando a expressão, temos:
Passo 3
Item (b)
Vamos trabalhar com a desigualdade de Taylor. Logo temos que:
Sendo que .
Como o intervalo fornecido no enunciado é , então temos que:
Conforme tabela do passo 1, temos que está decaindo no intervalo , logo podemos pegar o maior valor nesse intervalo como sendo:
Sendo assim, substituindo esse valor para , obtemos:
Passo 4
Item (c)
Aqui precisamos determinar o gráfico de:
Sabemos que:
Logo, temos que o gráfico de:
Vai ser o seguinte:
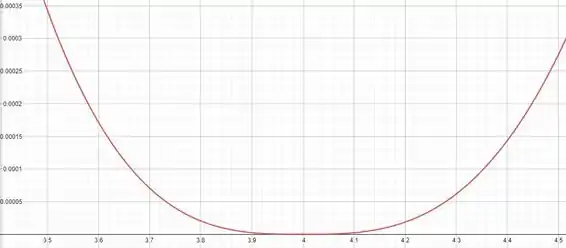
De acordo com o gráfico, o erro aparenta ser menor do que 0,00035 no intervalo especificado.
Resposta
