Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.11 - Ex. 4
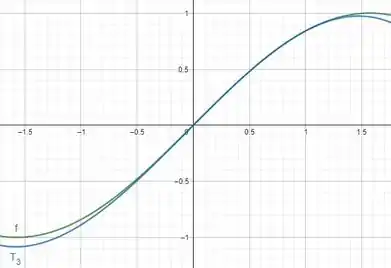
Encontre o polinômio de Taylor para a função ao redor de . Esboce o gráfico de e de no mesmo gráfico.
4.
Passo 1
Fala aí! Tudo show??
Olha só, o enunciado pede pra gente encontrar o polinômio de Taylor para a função ao redor de , além de esboçar o gráfico de e . Tudo belezinha, né?
A série de Taylor é dada por:
Onde serão as nossas derivadas que iremos fazer. No caso, faremos três derivadas, já que a questão quer .
Passo 2
Podemos reescrever a série de Taylor escrita no passo 1 como:
Sabendo os resultados da derivada de , então podemos jogar na nossa fórmula e assim, expandir:
E simplificando a expressão, obtemos:
Passo 3
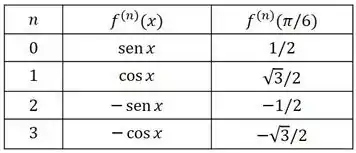
Agora, substituindo o valor de na expressão, obtemos os seguintes resultados:
E o gráfico contendo e é dado a seguir:
Resposta
Exercícios de Livros Relacionados
Prove que a série obtida no exercício 17 representa senh x para qualquer x .
Calcule a integral indefinida como uma série infinita. ∫ x 2 sen x 2 d x
Use a série binomial para expandir a função como uma série de potência. Espeficique o raio de convergência.
Encontre a série de Maclaurin de f (através de qualquer método) e o seu raio de convergência. Faça o gráfico de f e os seus primeiros polinômios de Taylor no mesmo gráfico. O que você percebe sobre a
Encontre a série de Maclaurin de f (através de qualquer método) e o seu raio de convergência. Faça o gráfico de f e os seus primeiros polinômios de Taylor no mesmo gráfico. O que você percebe sobre a