Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.18 - Ex. 4
Uma barra horizontal está localizada sobre o eixo dos , como mostra a Figura 8.105.
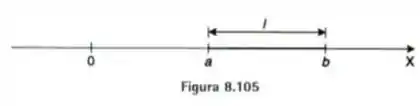
Se a densidade linear num ponto qualquer da barra é proporcional à distância desse ponto até a origem, determinar o valor da constante de proporcionalidade, de modo que a massa da barra seja
Passo 1
Sendo proporcional à distância desde a origem, a densidade linear pode ser escrita, na forma de função polinomial, da seguinte maneira:
Onde é a constante de proporcionalidade que queremos encontrar.
Já sabemos dos exercícios anteriores a seguinte expressão:
Passo 2
Integrando ambos os lados da sentença anterior, tendo como limite de integração o intervalo de a , temos:
Resposta
Exercícios de Livros Relacionados
Determine o valor médio de f x = 1 x em [ 1 , 2 ] .
A capacidade térmica Cv é a quantidade de calor necessária para elevar a temperatura de determinada massa de gás a um volume constante de 1 ºC, medida em cal/ºC.mol ( calorias por grau centígrado, por
Seja f uma função derivável em [ a , b ] . No Capítulo 2, definimos a taxa de cariação média de f ao longo de [ a , b ] como f b - f a b - a E a taxa de variação instantânea de f em x como f ' ( x ) .
Nos Exercícios de 47 a 50, ache o valor médio da função f no intervalo [a,b]. Nos exercícios 47 e 48, ache o valor de x onde ocorre o valor médio de f e faça um esboço.49. f x = 3 x x 2 - 16 ; a , b =
52. Para o circuito elétrico do Exercício 51, ache a raiz quadrada do valor médio de E 2 de t = 0 a t = π 3 . (Sugestão: use a identidade s e n 2 x = ( 1 - c o s ( 2 x ) 2 )