Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.6 - Ex. 16

Na barra do Problema 15, suponha que L = 30 ,   q u e   α ² = 1 e que a distribuição inicial de temperatura é f(x) = 30 – x para 0

  1. Encontre a temperatura u(x, t).
  2. Faça o gráfico de u em função de x para diversos valores de t. Faça, também, o gráfico de u em função de t para diversos valores de x.
  3. Como muda a localização do ponto mais quente da barra x m quando t aumenta? Desenhe o gráfico de x m em função de t.
  4. Faça o gráfico da temperatura máxima na barra em função de t.

Passo 1

Temos:

L = 30 ,   α ² = 1   e   f ( x ) = 30 - x ,   0 < x < 30 .

E a solução é dada pelo problema anterior:

u ( x , t ) = ∑ n = 1 ∞ c n e - ( 2 n - 1 ) ² π ² α ² t 4 L ² s e n [ ( 2 n - 1 ) π x 2 L ]

c n = 2 L ∫ 0 L f ( x ) s e n [ ( 2 n - 1 ) π x 2 L ] d x

Passo 2

Queremos achar c n :

c n = 120 ( 2 n - 1 ) ² π ² [ 2 c o s ( n π ) + ( 2 n - 1 ) π ]

Substituímos e achamos:

u ( x , t ) = ∑ n = 1 ∞ 120 ( 2 n - 1 ) ² π ² [ 2 c o s ( n π )   +   ( 2 n - 1 ) π ] e - ( 2 n - 1 ) ² π ² t 3600 s e n ( ( 2 n - 1 ) π x 60 )

Passo 3

Na letra b:

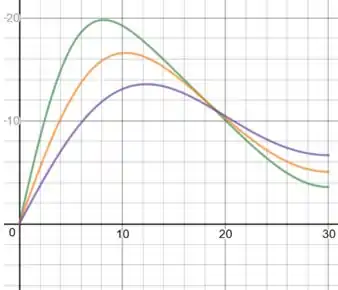
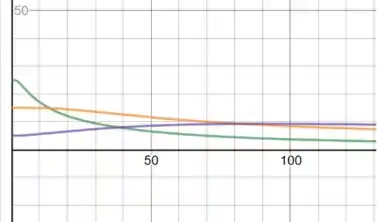
u versus t para x=5,15,25:

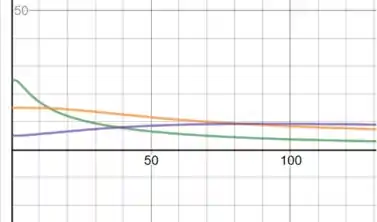
u versus x, para t=10,20,35:

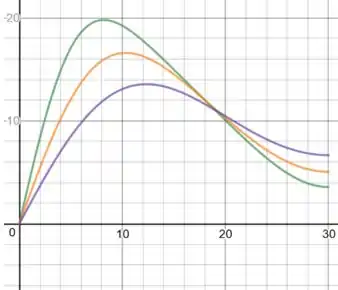
Passo 4

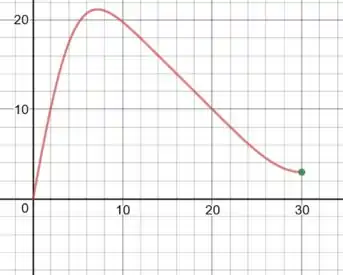
Na letra c:

Quando x=0, o tempo é 30 e quando x=30 o tempo é 104.4:

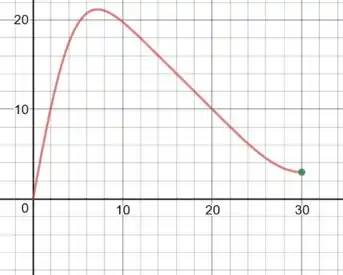
Passo 5

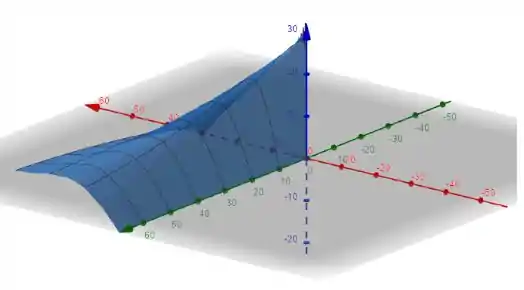
Na letra d:

O gráfico 3D é:

Resposta

  1. u ( x , t ) = ∑ n = 1 ∞ 120 ( 2 n - 1 ) ² π ² [ 2 c o s ( n π )   +   ( 2 n - 1 ) π ] e - ( 2 n - 1 ) ² π ² t 3600 s e n ( ( 2 n - 1 ) π x 60 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que α 2 = 1 e que s(x) = k na Eq. (i), com k constante. Encontre υ(x).Suponha que T 1 = 0 ,T 2 = 0 ,L = 20 ,k = 1 / 5 e que f(x) = 0 para 0
Considere uma barra com 30 cm de comprimento, feita de um material para o qual α 2 = 1 e cujas extremidades estão isoladas. Suponha que a temperatura inicial é zero, exceto no intervalo 5x10 , em que
Sejam α 2 = 1 e s ( x ) = k x / L na Eq. (i), em que k é constante. Encontre u ( x ) .Suponha que T 1 = 0 ,T 2 = 0 ,L = 20 ,k = 1 / 2 e que f(x) = 0 para 0
Considere o problema X ' ' + λ X = 0 ,X ' ( 0 ) = 0 ,X ' ( L ) = 0 . Seja λ = μ 2 , em que μ = v + i σ , com ν e σ reais. Mostre que, se σ ≠ 0 , então a única solução das Eqs. (i) é a solução trivial
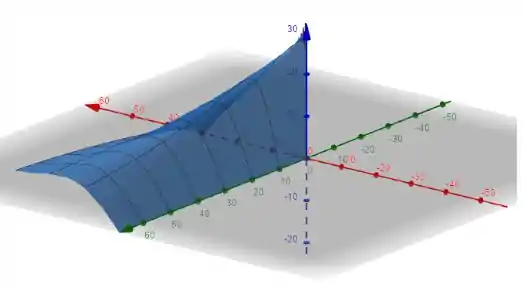
Considere uma barra uniforme de comprimento L com distribuição inicial de temperatura dada por f ( x ) ,0 ≤ x ≤ L . Suponha que a temperatura na extremidade x = 0 é mantida a 0°C, enquanto a extremida