Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.6 - Ex. 14

Considere uma barra com 30 cm de comprimento, feita de um material para o qual α 2 = 1 e cujas extremidades estão isoladas. Suponha que a temperatura inicial é zero, exceto no intervalo 5 < x < 10 , em que é 25°C.

  1. Encontre a temperatura u(x, t).
  2. Faça o gráfico de u em função de x para diversos valores de t. Faça, também, o gráfico de u em função de t para diversos valores de x.
  3. Faça o gráfico de u(4, t) e u(11, t) em função de t. Note que os pontos x = 4 e x = 11 estão localizados simetricamente em relação ao pulso inicial, mas os gráficos de suas respectivas temperaturas são bem diferentes. Explique fisicamente por que isso acontece.

Passo 1

Temos:

u x , 0 =   25 ,   no intervalo   5   <   x   <   10   ,

Onde:

0   ≤   x   ≤   30  

u x , 0 = 0 , em outro caso

E a solução é dada pelas fórmulas 35 e 37 na página 637:

u ( x , t ) = c 0 2 + ∑ n = 1 ∞ c n e - n ² π ² α ² t L ² c o s ( n π x L )

c n = 2 L ∫ 0 L f ( x ) c o s ( n π x L )

Passo 2

Temos:

L = 30 ,   α ² = 1 ,   c 0 = 25 3

e queremos achar c n :

c n = 50 n π ( s e n ( n π 3 - s e n ( n π 6 )   )  

Substituímos e achamos:

u ( x , t ) = 25 6 + ∑ n = 1 ∞ 50 n π ( s e n ( n π 3 ) - s e n ( n π 6 )   )   e - n ² π ² t 900 c o s ( n π x 30 )

Passo 3

Na letra b:

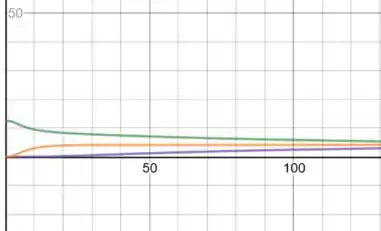
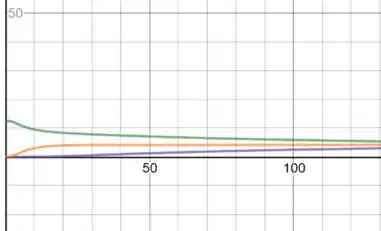
u versus t para x=5,15,25:

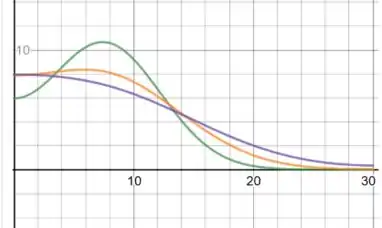
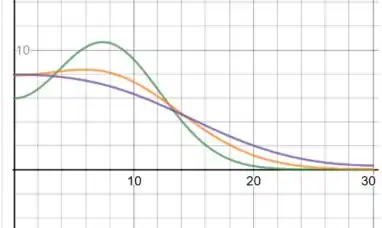
u versus x, para t=10,20,35:

Passo 4

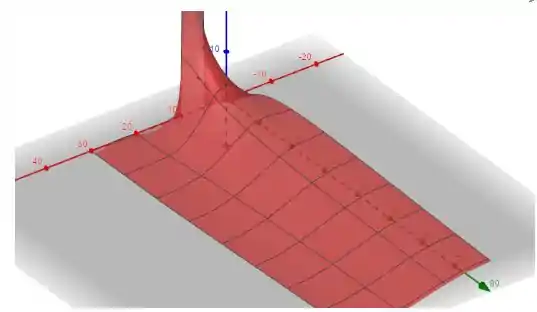
Na letra c:

u ( 4 , t )   e   u ( 11 , t )

Fisicamente isso acontece porque a temperatura aumenta na barra. Apesar de x=11 e x=4 são simetricamente alocados apesar do pulso de temperatura inicial, mais calor terá que fluir no intervalo [10,30] do que [0,5].

Resposta

  1. u ( x , t ) = 25 6 + ∑ n = 1 ∞ 50 n π ( s e n ( n π 3 ) - s e n ( n π 6 )   )   e - n ² π ² t 900 c o s ( n π x 30 )

  3. u ( 4 , t )   e   u ( 11 , t )

Fisicamente isso acontece porque a temperatura aumenta na barra. Apesar de x=11 e x=4 são simetricamente alocados apesar do pulso de temperatura inicial, mais calor terá que fluir no intervalo [10,30] do que [0,5].

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos problemas 31 a 34, resolva o problema de valor de contorno dado determinando a função de Green apropriada a expanssando a solução como uma integral definida. Use as equações de (i) a (iv) do probl
Considere o problema de valores de contorno r x u t = p x u x x - q x u + F x u 0 , t = T 1 u 1 , t = T 2 u x , 0 = f x a) Seja v x uma solução do problema p x v ' ' - q x v = - F x ,v 0 = T 1 ,v 1 =
Neste problema, vamos explorar um pouco mais a analogia entre problemas de Sturm-Liouville de valores de contorno e matrizes auto adjuntas. Seja A uma mátria autoadjunta n × n com autovalores λ 1 , …
O método de expansão em autofunção é usado, muitas vezesm oara oriblemas não homogêneos relacionados com a equação de onda ou sua generalização. Considere o problema r x u t t = p x u x x - q x u + F
Considere o problema de valor de contorno - d 2 y d s 2 = δ s - x ,y 0 = 0 ,y 1 = 0 . onde s é a variável independente, s = x é um ponto definido no intervalo 0s1 e δ é a função δ de Dirac (veja a seç