Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.1 - Ex. 9
9 -
Passo 1
Considere o sistema:
a)
Vamos assumir como a solução do sistema. Portanto iremos substituir esse valor no sistema.
Passo 2
Os valores são as raízes da equação.
Portanto, os autovalores são e .
Passo 3
Quando , a equação fornece,
Simplificando a primeira linha, temos:
Cada linha gera a condição:
O autovetor correspondente ao autovalor é: .
Passo 4
Agora, encontre o segundo vetor autônomo linearmente independente correspondente a . O vetor generalizado satisfaz a seguinte relação .
Simplificando a primeira linha, temos:
Cada linha gera a condição:
Vamos definir (constante arbitrária) para obter .
Então o vetor resultante é:
O segundo termo é um múltiplo de , portanto, pode ser descartado.
Então .
E, portanto, a solução geral é:
Onde são constantes arbitrárias.
Passo 5
b) Agora os autovalores são iguais a um autovetor independente, então o valor crítico
é um nó inadequado. Como os dois valores próprios são positivos.
Portanto, o ponto crítico é um nó impróprio instável.
Passo 6
c) O plano de fase do diferencial fornecido pode ser desenhado abaixo:
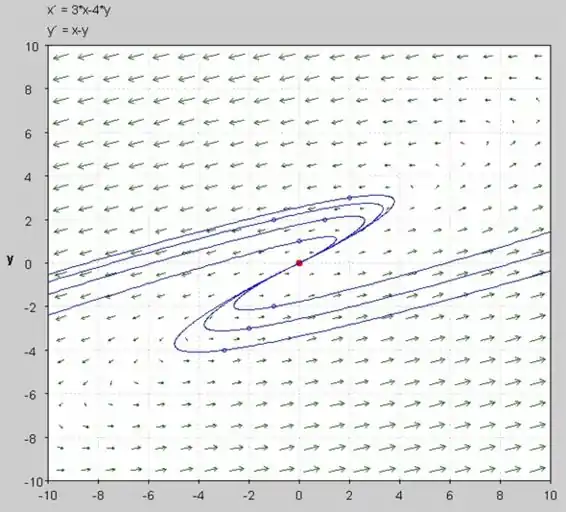
Agora, o esboço do gráfico de por é mostrado abaixo:
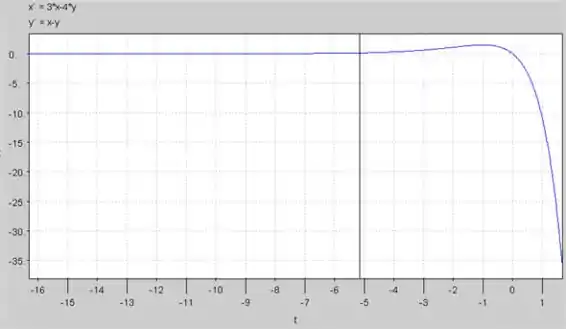
Da mesma forma, podemos esboçar o gráfico de por é mostrado abaixo.
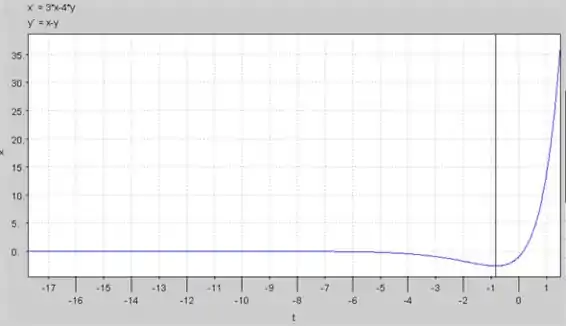
Passo 7
d) O esboço das trajetórias é mostrado abaixo:
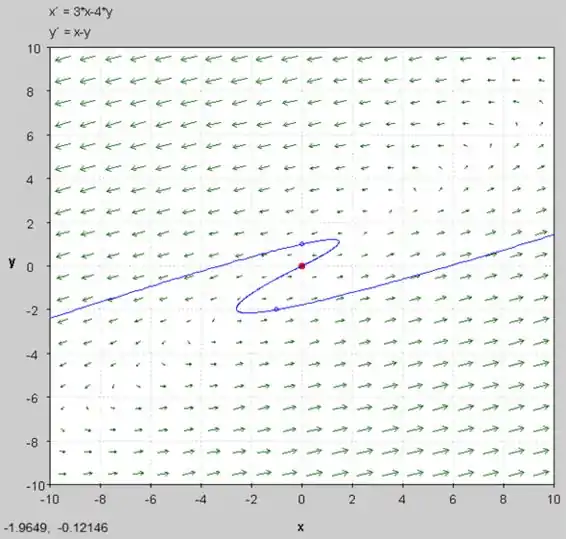
Resposta
- Os autovalores são e .
- O ponto crítico é um nó impróprio instável.
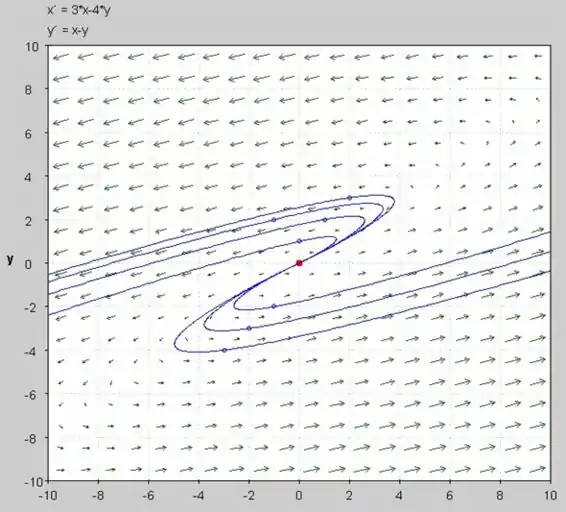
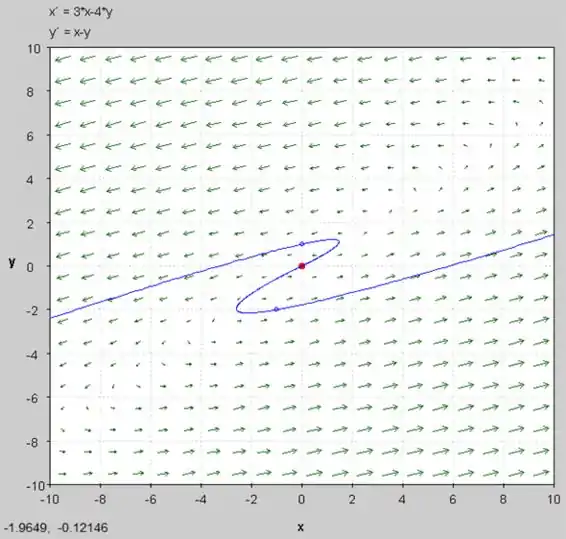
O autovetor correspondente ao autovalor é:
O autovetor correspondente ao autovalor é: