Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 6.3 - Ex. 1
Em cada um dos problemas de 1 a 6, esboce o gráfico da função dada no intervalo
Passo 1
Nós temos, por definição que
Nós temos: , e , isso significa que temos os respectivos , e , que são os subíndices dos intervalos.
Precisamos de intervalos que são menores que . Intervalo entre e , e entre e .
Quando :
Reorganizando a matriz com os resultados:
O rascunho do gráfico pode ser dado analisando o eixo das abscissas como e das ordenadas como . Para todo valor menor que , a função será constante em Para valores de entre 1 e 3, a função se comporta de maneira constante em 1. Para valores entre 3 e 4, a função é constate em 3, e para valores maiores que a função será constante em .
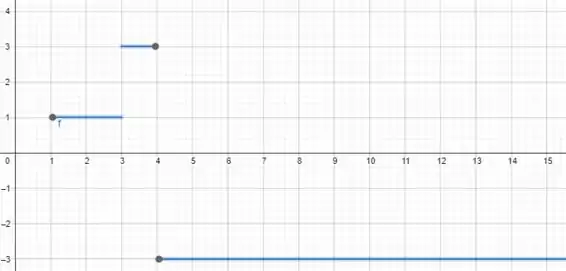
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use os resultados do Problema 25 para encontrar a transformada de Laplace inversa da função dada. F ( s ) = 1 9 s 2 - 12 s + 3
Em cada um dosproblemas de 7a12:(a) Esboce o gráfico da função dada.(b) Expressef ( t ) em termos da função degrau unitário u c ( t ) . f t = 1 ,0 ≤ t1 - 1 ,1 ≤ t2 1 ,2 ≤ t3 - 1 ,3 ≤ t4 0 ,t ≥ 4
Em cada um dosproblemas de 13a18, encontre a transformada de Laplace da função dada. f t = 0 ,tπ t - π , π ≤ t ≤ 2 π 0 ,t ≥ 2 π
Em cada um dosproblemas de 7a12:(a) Esboce o gráfico da função dada.(b) Expressef ( t ) em termos da função degrau unitário u c ( t ) . f t = 0 ,0 ≤ t3 - 2 ,3 ≤ t5 2 ,5 ≤ t7 1 ,t ≥ 7
Em cada um dosproblemas de 7a12:(a) Esboce o gráfico da função dada.(b) Expressef ( t ) em termos da função degrau unitário u c ( t ) . f t = t ,0 ≤ t2 2 ,2 ≤ t5 7 - t ,5 ≤ t7 0 ,t ≥ 7